一个任何样本量下比UMVUE还要“好”的有偏估计量！这一颠覆经验认知的反常现象，被称为Stein's paradox。

本人没有能力开拓什么，只能综合前辈们的观点尽量感悟；没有打算、更没有能力深入研究收缩估计，不过是对Stein's paradox的奇怪现象感到诧异，来了兴趣，所以查阅多手资料后写下了本文。

本文主要参考文献
把他们列在文首，只因为我看来这些文章比本文更有价值，推荐参考

ESTIMATION WITH QUADRATIC LOSS - Yale University

1961年Willard James与Charles Stein的文章，在这里James-Stein估计被首次提出，点击此处下载论文。

大规模推断讨论班：经验贝叶斯与 James-Stein 估计量 - GitHub

这篇文章非常系统地从经验Bayes观点引出了Stein理论与Robbins理论，读完后收获颇丰，本文也有所参考。也说明了，所谓“频率学派”、“贝叶斯学派”的对立，“贝叶斯世界观”等描述并不准确，频率方法和Bayes方法不是水火不容的，统计学发展到今天，他们本身的界限就比较模糊。

赵世舜. 矩阵加权估计及James-Stein估计的再研究 [D]. 吉林：吉林大学，2006.

感谢这篇博士论文为我提供的帮助，第二章定理证明的思路是源自于这份文献的；好像在2017年赵已经在吉林大学数学学院升任教授职务了。由于知网下载文献得付费，我用学校的渠道下载了下来并上传到了网站，点击此处查看这篇论文。

~~本文不是正经的论文，懒得划出具体的引用😊~~以上文献本身亦引用了较多文献，如果有兴趣，不妨也读一读。

本文用到了一些缩写：MLE指极大似然估计，UMVUE指一致最小方差无偏估计，MSE指均方误差，G-M定理指高斯-马尔可夫定理。

the James-Stein Estimator

众所周知，元正态分布总体数学期望的MLE是样本均值，即，是一个十分符合直觉且自然的统计量，由于他的简单直接，通常多数人也会采取他为总体期望的估计。事实上，由于正态分布族系指数族，并且是是充分完备统计量，故根据Lehmann–Scheffé定理，样本均值是总体期望的UMVUE——这意味着，在无偏估计中样本均值的方差是最小的，可见样本均值是一个性质优良的估计。进一步地，达到了Cramer-Rao下界。

但是，这并不意味着样本均值在任何意义下都是最“好”的！1961年由Willard James和Charles Stein基于1956年Charles Stein提出的早期版本所改进得到的James-Stein estimator（下简称JSE）就是这样一个例子，当用表示的样本均值的标准误时，有式可视为样本量的推广，如果只有一个样本，则退化为相较于样本均值，JSE的方差显著减小了；尽管失去了无偏性，但渐进无偏，最重要的是在情况下其MSE严格小于样本均值，这时JSE严格一致优于样本均值，这一现象也被称为Stein's paradox。~~当p=2时显然JSE等价于样本均值。~~

这个结论第一眼看起来真的出人意料！这似乎违背经验，毕竟在我们的印象中，寻找、构造UMVUE一直都是统计学家的“毕生追求”，然而JSE的出现却表明，在非无偏估计家族中、在某些情况下，我们或许有比UMVUE更好的选择（这具体取决于我们在特定情境下如何定义“损失”标准）。

这也深刻地说明了，UMVUE其实并没有设想的那般“绝对的好”，当我们把眼光放宽到无偏估计，可能还有更“好”的估计在等着我们发掘。JSE就揭示了，当维数大于2，样本均值作为UMVUE就未必还是最好的估计！换句话说，在低维可容许的样本均值，在高维是不可容许的，这侧面印证了低维直觉放在高维中很可能是错误的，高维统计中还有很多这样的例子。

Tip: 由于正态分布的样本均值仍服从正态分布，为简便起见，后文中如若未做特别说明，则只考虑的情况，不再区分与。

James-Stein型估计的风险

这里将按照赵世舜在其博士学位论文中所给出的，仿照1981年Stein、1990年Brandwein与Strawderman给出的较为简单的证明，证明当、且时，James-Stein型估计的风险一致小于的；并且，当时，估计的风险达到最小，若进一步，这时估计正是JSE，即。

~~看过1961年Willard James与Charles Stein的论文原文，这部分没有看懂，所以不按那最古老的方法证明风险一致地小了。~~

引理 1 (成平等，1985) 当，可微且，有在后文的证明中只会用到的情形。

定理 1 以二次损失定义风险，设，则当、且时，估计的风险均小于的风险，且的风险为易见当、，，该定理更具有一般性。

首先容易知道，观察，根据引理 1，有将式代入式，则不过，至今没有很好的办法确定最佳的、。赵世舜在他的博士学位论文中指出，有理由认为选择合适的是比取更“好”的，尽管JSE中取。

值得说明的是，即使是未知的，用的估计代替，James-Stein型估计的风险依然一致小于，这就不再赘述了。

可视化JSE与MLE的估计效果

通过下述代码直观地可视化JSE与MLE估计效果上的差异，

import numpy as np
np.random.seed(1)

mean = [0,0,0]
sigmaSq = 1
N = 1
p = len(mean)

df = np.random.multivariate_normal(mean, sigmaSq*np.identity(p), size=N)

class Estimator():

    def JSE(self, X, sigmaSq=1):
        X_bar = np.average(X, axis=0)
        XX = np.dot(X_bar, X_bar)
        sigmaSq_bar = 1 / df.shape[0]
        theJSE = (1-(df.shape[1]-2)*sigmaSq_bar/XX)*X_bar
        return theJSE

    def MLE(self, X):
        return np.mean(df, axis=0)

    # sklearn.metrics.mean_squared_error
    def MSE(self, X_estimate, X_actual):
        X_est = np.array(X_estimate)
        X_act = np.array(X_actual)
        return np.sum(np.square(X_est-X_act))/X_est.size

    def compare(self, X, X_actual, show=True):
        estimate_JSE = self.JSE(X)
        estimate_MLE = self.MLE(X)
        MSE_JSE = self.MSE(estimate_JSE, X_actual)
        MSE_MLE = self.MSE(estimate_MLE, X_actual)
        if show == True:
            print("JSE: {}, the MSE: {:<8f}".format(estimate_JSE, MSE_JSE))
            print("MLE: {}, the MSE: {:<8f}".format(estimate_MLE, MSE_MLE))
        return [estimate_JSE, estimate_MLE, MSE_JSE, MSE_MLE, MSE_MLE/MSE_JSE]

est = Estimator()
summary = est.compare(df, mean)

为保证结果可复现，设置种子np.random.seed(1)，部分测试样例如下表：

N	N=1 1	N=20 1	N=10 `np.repeat(1,50)` 4	N=1000 1	N=5 1	N=1 `np.random.rand(10)` 1
MSE(JSE)	0.531834	0.030650	0.321131	0.001485	0.000059	0.290441
MSE(MLE)	1.097236	0.030969	0.373426	0.001487	0.122682	1.291636

由于元正态分布的样本均值也服从元正态分布，而且样本量越大，越小，所以理论上JSE与MLE都会逐渐贴近总体期望。以np.random.rand(10)作为总体均值，观察样本量从1到30时二者的变化。

import matplotlib.pyplot as plt
np.random.seed(520)

mean = np.random.rand(10)
sigmaSq = 1
N_max = 30
p = len(mean)

mseJSE_n = np.empty(N_max, float)
mseMLE_n = np.empty(N_max, float)

for n in range(1, (N_max+1)):
    df = np.random.multivariate_normal(mean, sigmaSq*np.identity(p), size=n)
    summary = est.compare(df, mean, show=False)
    mseJSE_n[n-1] = summary[2]
    mseMLE_n[n-1] = summary[3]

plt.plot(mseJSE_n, 'o-', label='MSE(JSE)', linewidth=2)
plt.plot(mseMLE_n, 'o-', label='MSE(MLE)', linewidth=2)

plt.xlabel('Sample size', fontsize=14)
plt.ylabel('MSE', fontsize=14)
plt.title('Comparison', fontsize=16)
plt.legend(fontsize=12)

plt.tick_params(axis='both', which='major', labelsize=12)

# plt.savefig('visual comparison.svg', dpi=1200, format='svg')
plt.show()

可视化结果如下：

可以看出，当样本量较小的情况下，在MSE准则下JSE是明显优于样本均值的，随着样本量的增大二者差异逐渐减小，均向收敛。不过在前面本文已经证明了，JSE是一致优于样本均值的（而不仅在小样本下）。当样本量较小时，JSE大大优于MLE。

抛开MSE准则不论，从数字的差异上也能直观感受到JSE更加“精准”。对正态总体产生的样本量为2的样本进行均值估计，观察估计向量的值：

JSE: [ 0.20985719, 0.09654112 ,-1.07700422], the MSE: 0.404433
MLE: [0.27568837, 0.12682561, -1.41485522], the MSE: 0.697968

显然，JSE更接近总体均值。

当总体均值的长度与方差较小时，他们的变化对JSE与MLE间优劣的差异几乎没有影响，

二者MSE随着总体均值长度的增大而稳定增大且速率越来越快；
随方差增大震荡增大.

以下为随机抽取的可视化典型样例：

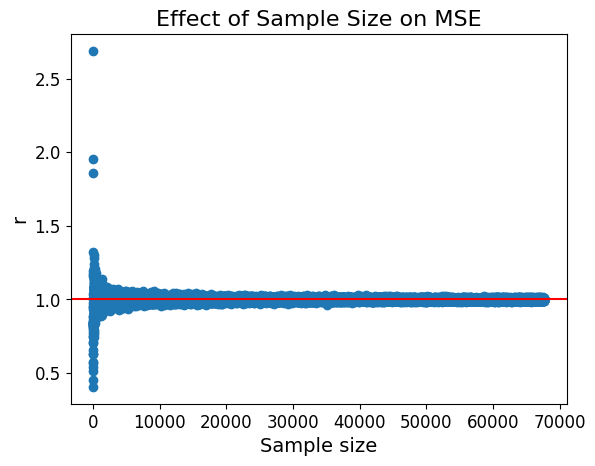
为探究何种因素会使影响JSE与MLE的相对估计效率，记MLE与JSE的MSE比值为，越小表明JSE越优于MLE。在前文代码基础上进行修改，进行模拟试验。下列出典型样例：

由此可知，在其余条件控制不变的前提下，

伴随的增大，很快收敛于，二者无明显优劣；
伴随的增大，趋向于，但在较小时JSE优于MLE，随后优势被渐渐削弱。考虑到控制在、样本量控制在(图中是的情况)，当充分大时讨论估计的优劣没有太大价值，因此可以认为JSE优于MLE；
伴随维数的增大，将收敛到一个明显小于的值，JSE显著优于MLE；
伴随样本量的增大，在附近跌宕起伏且波动幅度不可忽视，估计相对优劣的变化不规律，但是在样本量较小时JSE仍优于MLE，随后优势被渐渐不明显；
无论如何，在绝大多数情况下，JSE的平均风险不超过MLE；
模拟中并未测试但不排除可能的影响因素：变异系数.

Shrinkage Estimation与正则化

JSE是一种Shrinkage estimation，中文一般译作收缩估计、压缩估计。收缩估计第一次在Willard James和Charles Stein的《Estimation with Quadratic Loss》中出现，正是在这篇文章中提出了本文的对象JSE，不过“收缩”一词直到1983年Copas在《Regression, Prediction and Shrinkage》中才被提出，在这篇文章中他这样定义了收缩：

The fit of a regression predictor to new data is nearly always worse than its fit to the original data. Anticipating this shrinkage leads to Stein‐type predictors which, under certain assumptions, give a uniformly lower prediction mean squared error than least squares.

压缩估计通常会以偏差的较小增长换取显著更小的方差，这被称为方差-偏差权衡策略；换句话说，用均值的偏移换取更小的置信区间。收缩在Bayes推理和惩罚似然推理中是隐式的，在James–Stein型估计的推理中是显式的；JSE可谓是收缩估计的开山之作，同为收缩估计的还有岭估计(ridge estimator)、LASSO估计以及他们的一系列改进，这些都是比较新的方法。

关于收缩估计还有个更简单的例子，通常样本方差通过给出，将自由度作为除数是为了保证估计的无偏性，使用其他的数作为除数会导致估计有偏（一般要保证统计量仍是渐进无偏的），但有可能会得到更小的MSE。至于选取什么数、选取怎样的收缩能减小MSE，一般而言是由总体的峰度决定的，譬如对于正态分布，取为除数时会得到最小的MSE，这就是总体方差的一个收缩估计。

从正则化的观点看，收缩是一种正则化惩罚的形式，也可以说正则化是实现收缩的手段之一，通过（将参数向或'null'）移动，减轻统计模型的过拟合。将分量向着彼此靠近也是一种收缩，这代表着差异向着移动了——JSE便是将样本均值的每个分量向零收缩，其数量与其与零的距离呈正相合。

JSE的形式为，令为shrinkage factor，那么JSE可以看作在样本均值的基础上进行了“收缩”，形式上为，收缩程度由收缩因子决定：
相较于样本均值将每个维度的分量分开计算均值，JSE把分量们整合起来进行估计.

尽管JSE如此“年迈”，但在很多情景下仍发挥着不可或缺的重要作用，后续提出的许多新压缩估计也是基于JSE的。不过据李婷婷老师所言，似乎收缩估计这块并没有太多人在研究了。看起来，起码是我校是没有老师在做的。

JSE的经验Bayes推导与解释

最初JSE是由Willard James和Charles Stein通过经验Bayes估计(empirical Bayes methods)导出的，正如前文所述，那时还没有诞生shrinkage的概念。在此，我希望通过经验Bayes的解释，让JSE在Bayes框架里看起来更自然。这也说明，选择合适的先验，Bayes估计可以比MLE更“好”——尽管MLE本身也和Bayes框架是兼容的。

与前文类似地，只考虑的情况，若将替换为即可。假设观测值来自总体期望为的正态分布，在的条件下；而本身服从某种分布，记为，根据Bayes公式，有 $后验概率先验概率似然边际概率$ 其中，先验(prior)是事先给定信息，是试验前已知的信息；似然(likelihood)则是在条件下的分布，是观测值，是试验中获取的信息；边际概率又称边缘概率，可以视作排除了的影响后的分布，即无论取何值的“平均”的分布(想想看，这不就是在求期望么？)；后验(posterior)则正是经过试验后对先验的更新与调整，在先验信息下经过试验获得并加入更多的信息后，得到了更准确的估计，这便是后验信息，正是当下所需要的。

既然服从正态分布，的MLE——样本均值也服从正态分布，那么有理由假设亦服从正态分布。若令，取先验，则可以计算后验的分布，因此，另外可以解出边际概率。边际概率的积分计算需要一些积分技巧，具体推导可以类比讨论班给出的过程。

根据解出的后验分布，可以得出在先验下，总体期望的Bayes估计为接下来的问题是，也是未知的，所以应当寻找一个对的恰当的估计，于是很自然地想到利用方差的无偏估计代替方差，这一方法在构造多种正态检验统计量中是关键中的关键。

现构造的估计，利用前文给出的边际概率，容易知道，因此。根据逆分布的性质，从分布出发，利用可以导出：即：将式代入式，得式和式是完全相同的，至此，本文从Bayes估计的角度导出了JSE，提供了JSE的Bayes解释。从这个视角看，常数也就没那么突兀了，甚至可以说是由逆分布均值的性质所决定的。

注：式中可以看出是的无偏估计，但参考Duke大学STA732统计推断讲义第11节Empirical Bayes and Hierarchical Bayes，其实还是的UMVUE。

最后，上文的推导中运用了自由度为的逆分布均值为的结论，在此补充中心化逆分布的均值与方差的解法，来源StackExchange：

将JSE推广至更佳的矩阵形式

赵世舜在博士学位论文中完成了这项工作，他证明了可以将JSE推广至矩阵形式，而且保持了良好的性质。

推广的思想与动机是，根据随机变量二次型期望理论，当，有，因此可以将JSE的估计对象改写于是联想到将估计的形式推广为如下向量表示：将未知参数用相应的估计量替代即可得到JSE的矩阵推广形式。

赵世舜证明了JSE的矩阵推广形式拥有至多与JSE相等的的MSE，下展示赵世舜博士学位论文中的这一部分结果：

此外，还有：

该定理的证明参见原文。

JSE与OLS

如果线性模型的残差被假设服从正态分布，很容易把JSE应用到线性模型回归系数的估计中。推导与证明的过程不再赘述，仿照着上文即可，只给出结果：其中是回归系数的个数，是设计矩阵；当G-M定理的条件成立且时，该估计一致优于OLS。

线性模型的JSE推导与诸多性质的证明本文不再深究了，可以参考：

James-Stein estimation，若无法访问则请点击此处；
James–Stein estimation problem for a multivariate normal random matrix and an improved estimator

本文到这里正式结束了。或许后来的我随便翻看着本文，会感慨：原来读本科的时候，我还有毅力去尝试着学习。

本文的写作中参考了许多相关文献，真正的原创大概只有第三章的可视化与第五章的证明，事实上第五章也只是在其他文献基础上做了推广的推导，在原文中只展示了的情况。

二三事

The James-Stein Estimator