线性回归的理论与应用

方便起见，本文用代表，其中是或范数，用RSS或SSE表示残差平方和，用SSR表示回归平方和，用SST表示总平方和，用OLS表示最小二乘法，用MLE表示极大似然估计，并采用下分位数的记号。

本文最初是作为本科阶段期末考试的复习总结，★代表考试中重要程度，●代表不会刻意作为考点，◆代表只考察解读或名词解释，不考察理论推导与证明，最后▲代表虽然是复习课上明确提到的必考内容，但会做变形或考察类似题目。由于本文作于作者大三时期，且原先的目的也只是系统地总结回归分析考试考点，所以本文不会十分深入地探究太多涉及底层理论的内容；文章侧重点更多的还是线性回归本身的理论，所以一些应用中的处理方法和可能遇到的问题并没有太多诠释。

不过，后来断断续续扩写补充了相当一部分本科课程以外的内容，如果读者仅仅希望将本文作为（西南大学统计系）期末考试的复习笔记，则没有任何记号标记的标题下的内容，均可以忽略。

参考书目有：

• 学院的本科授课教材，即王松桂等人所编著的《线性统计模型：线性回归与方差分析》
• 同时也参考了茆诗松等编著的《概率论与数理统计教程 (第三版)》与贾俊平等编著的《统计学 (第8版)》
• 若干网络资源与Wiki百科

在此感谢我的回归分析任课教师徐文昕老师。

---

前言

最小二乘法有着极为广泛的运用，他的优良性质由高斯-马尔可夫定理所保证；除此之外，如果残差还独立同分布于正态分布，则此时OLS等价于MLE。即便残差并不服从正态分布，只要满足高斯-马尔可夫定理的基本条件，那么OLS就是最优的无偏估计，这说明了线性回归的强大之处。

然而在许多情形下，相对于一些其他的方法（尤其是非参数方法），OLS在稳健性方面略显疲态。考虑到最小二乘法的损失函数为RSS，一旦样本数据中出现了严重偏离总体的异常点，误差将会在被平方后大幅增加。这种情况下，如果依然希望最小化RSS，可能导致OLS的值因此而发生较大的变化，使得回归曲线偏向于异常点，换句话说：OLS是对异常值十分敏感。

让我们把目光转向最小一乘法。最小二乘法的损失函数为，而最小一乘法的损失函数为，从损失函数的形式上看，如果出现异常值，显然RSS产生的惩罚更严重，而最小一乘法的惩罚则较轻（毕竟，在时，），受到的影响相对更小。当然，这也是个比较粗浅的观点，实质上最小一乘回归对应中位数回归，而最小二乘回归对应均值回归——最小一乘回归是一种特殊的分位数回归，分位数取二分位数，即中位数。鉴于本文并不是非参数统计的详解文章，这里就不再赘述最小一乘法的更多性质。写下这些文字，我想表达的是：最小一乘法与最小二乘法之间，本身并无绝对的优劣之分，至于哪种方法表现更好，视情况与需求而定。

另外，最小二乘线性回归出现较早、结构简单，是一种经典而传统的回归方法，预测能力较差，远远不及SVM等一众现代方法，这是他结构太过简易导致的，尤其是站在大模型正值风口的今天。但是，也正因如此，线性回归时至今日仍有非常广阔的运用，主要原因是其结构简单、模型解释性强，回归参数也有着非常明确的统计意义与现实背景，通常在不以精准预测为目的的数据分析任务中都会看到线性回归的身影——单单是回归系数的符号就已经能说明太多信息，譬如研究课后活动类型与花费时间对学生成绩的影响、探究某组合药物各成分的剂量对实验用小白鼠的影响。

最后，大名鼎鼎的方差分析也是一种线性回归，不过是较为特殊的线性回归，自变量均为分类数据；既含有离散的分类变量又含有连续的数量变量的线性回归，称为协方差分析。

方便起见，本文只讨论最基本的线性模型，且不考虑交互项。不过，读者很容易就能把本文的理论推广、扩展到这些内容上去。

一元线性回归公式速查

由于一些其他的教材针对一元线性回归使用了特别的记号，而在实际的理论和应用中，相当一部分数据以这类教材所采取的记号形式给出。为方便查阅，在此直接给出这种别于本文符号体系下的一元线性回归的全部基本公式，于下一小节再做详细证明。

在有的教材中，针对一元线性回归模型，规定： 于是

另外，在高斯-马尔可夫定理的条件下，有 相应的，，，，在此一并给出参数显著性检验统计量：

此外，对一元线性回归还有所谓相关系数检验，记为样本Pearson相关系数，置原假设为相关系数，则 对一元线性回归而言，三个检验是等价的。

置信区间同理构造：

的置信区间与预测区间是有区别的。若记回归模型为，则的“置信区间”是的置信区间，即平均值的置信区间，是总体的、概括性的区间，而的“预测区间”是的置信区间，即考虑了误差项后真实值的置信区间，是单独的、个体的区间，这也是为什么预测区间范围要广于置信区间，因为他包含了置信区间。

在此重申置信度为置信区间的含义：随机抽取组样本，理论上应有组样本构造的随机区间中包含了参数真实的值。

对一元线性回归而言，Pearson相关系数的平方等价于拟合优度。

一元线性回归非矩阵代数全证明

后文中对多元线性回归性质的证明都是利用向量代数与矩阵代数进行的，这里不使用向量代数与矩阵代数的方法，仅用最最基本的线性代数基础来完成一元线性回归大部分基本性质的证明。

同上文，为方便讨论，依然做如下规定：

---

1. OLS公式：

   证：损失函数为，分别令对的偏导为，有 整理即得 这是一个关于未知数的二元非齐次线性方程，由克拉默法则解得 对等式两边同除，得

2. 残差和

   证：由于，根据等式易得。

3. 证：由于，根据等式易得。

4. （前提：残差服从正态分布，否则只能计算均值与方差）

   证：这里我们把视为常数而将视为变量，也就是说将认为是人为选取的、是确定的，而将每个对应的视为包含球形扰动项影响的随机变量，于是由前文推导的估计公式，我们只需要讨论的性质。

   由于我们只有残差分布的信息，故将拆分，直到出现残差： 注意到式中均为常数，唯一的变量为，可见是有限个正态分布的线性组合，因此也服从某个正态分布，即具体的分布由其均值与方差唯一确定，下计算其均值与方差。

   由条件，有

   因此，

   综上所述，有

5. 与相互独立（前提：残差服从正态分布，否则只能保证与不相关）

   证：由于中仅有球形扰动项样本均值为变量且服从正态分布，因此也服从正态分布。考虑到亦服从正态分布，证明两个正态变量相互独立等价于证明二者不相关，所以证即可。 在前文中已证明，又已证明，所以，从而 也就是说，与相互独立。

6. （前提：残差服从正态分布，否则只能计算均值与方差）

   证：由于且在上文已证明，因此作为正态分布的线性组合，也服从某个正态分布，下计算其均值与方差。 在上文中已证明与相互独立，因此，从而有 综上所述，有

7. 证：这里依然需要用到前文已证明的与不相关，有

8. （前提：残差服从正态分布，否则只能计算均值与方差）

   证：由于，易知也服从正态分布，下计算其均值与方差，其中对方差的计算需要用到上文中已证明的。

   综上所述，有

9. 证：为总平方和，为回归平方和，为残差平方和， 按定义易见，下证。

10. （前提：残差服从正态分布）

    证：这部分的处理是比较复杂的，首先计算。在计算前，又需要先计算。 当残差服从正态分布时，，因此，从而，也就是说 从而 接下来计算。如果考虑，则步骤又会像上文计算一样繁复了；应当考虑，利用前文已证明的性质快速解决问题。 由于，所以 于是

11. 证：这是线性回归的平方和分解公式，

12. （，前提：残差服从正态分布）

    证：之所以取的估计，是因为，所以实际上要证的是。考虑到的期望不太好处理，可以利用上文中已证明的平方和分解与已计算的、来间接计算。

13. 当，（前提：残差服从正态分布）

    证：先证，当时有，从而 接下来证。根据基本的数理统计知识，可以知道 由于是一系列零均值正态分布平方的线性组合，理应也服从某个卡方分布。利用平方和分解公式容易知道所服从的卡方分布自由度为，因此

14. 至此一元线性回归的大部分基本性质证毕，检验统计量的构造与置信区间便都是显而易见的事情了。这里作一个简单总结，其中为样本的Pearson相关系数，，并设原假设为 “”。

第一章：引论

这里用表示未知变量的个数，则包含截距项的元线性回归中，。有的文献中，会规定包含截距项的元线性回归中，请注意区分。

★ 1.1 线性回归模型

若与（维向量）存在线性关系，则可建立元线性回归模型 称为截距项，为回归系数；为随机误差，包含了可能影响取值但不可观测或未被考虑的潜在协变量。

称为经验回归方程。

另外，线性模型是可加减的，不过这应该毋需多言（可以尝试找出，当条件减弱到何种地步时线性模型不再可以加减？）。

---

★ 1.2 线性模型的经验回归方程解读

由于，所以在保持不变的情况下，每增加个单位，则增加个单位；

进一步的，在高斯-马尔可夫定理条件下有，因此：不变，每增加个单位，平均增加个单位（对应经济学中“边际”的概念）。

同理，实际上当不变、每增加个单位，平均增加个单位；对于，只需注意到他代表的正是当回归系数都取时的取值

---

★ 1.3 半对数模型(Ⅰ)的经验回归方程解读

该模型在生存分析的语境和条件下也被特称AFT模型，即加速失效模型。

等价于对因变量做的Box-Cox变换的线性模型（能降低原线性模型“异方差”程度），我们有 此式意味着在保持不变的情况下，每增加个单位，则增加；

由于在高斯-马尔可夫定理的条件下有，所以：不变，每增加个单位，平均增加。

对于同理

---

★ 1.4 半对数模型(Ⅱ)的经验回归方程解读

等价于对因变量做的Box-Cox变换的线性模型（能降低原线性模型“异方差”程度），我们有 此式意味着在保持不变的情况下，每增加，平均增加个单位；

由于在高斯-马尔可夫定理的条件下有，所以：不变，每增加，平均增加个单位。

对于同理

---

★ 1.5 双对数模型的经验回归方程解读

等价于“不仅对因变量做的Box-Cox变换同时对自变量取对数的线性模型”，此举能大幅降低原线性模型“异方差”程度，我们有 此式意味着在保持不变的情况下，每增加，则增加；

由于在高斯-马尔可夫定理的条件下有，所以：不变，每增加，平均增加（对应经济学中“弹性”的概念）。

对于同理

---

★ 1.6 多项式回归

p8 例1.1.4：单个变量的多项式回归仍属于线性回归模型，假设与之间有的关系，令，，，于是 得到了一个线性模型。

由此可以看出：线性模型的特征是关于回归系数，，，是线性的。

★ 1.7 方差分析简介

这里主要对单因素方差分析作概括性的简介。实质上，方差分析（ANOVA）是特殊的回归，较之回归分析，方差分析特别针对为连续型变量、​为离散型变量的情况。

方差分析的核心与底层逻辑即 “多元正态分布均值的检验”，二者在某些场合下是等价的问题。

方差分析是特殊的线性回归，其自变量类型为分类数据；如果线性模型的自变量类型同时包含了分类数据与连续数值数据，则称模型为协方差分析。从某种意义上说，方差分析即是总体均值的检验。

方差分析和线性回归有着极大的相似，例如他们的检验统计量分别为和，本质上其实并无二致。本文不多赘述方差分析，因为方差分析往复杂了说同样需要很大的篇幅，本文更多的还是关于连续数值的线性回归。

下面给出最简单情形的单因子方差分析过程，多重比较、多因子方差分析等不在此涉及。

假设数据共计组，每组包括次试验，则

方便起见，下用表示，用表示，用表示，用表示自由度，称为均方，指平均每个自由度上的偏差平方和，如。

构造检验统计量为： 拒绝域：

参数估计：，

的水平均值的置信区间：

称下表为方差分析表： 重复数不等时，将替换为​即可。

至于双因素的方差分析、多因素的方差分析，这里就不深入讨论了。

第二章：随机向量

● 2.1 矩阵代数：向量函数与矩阵函数偏微分

同样地有链式法则。

本文约定按分子布局，即认为分子是列向量、分母是行向量（标量统一被认为是行向量）。

题外话：在我们对OLS各种性质的推导中，要利用好一定是对称的半正定矩阵.

● 2.2 随机向量二次型的期望

记、，为对称阵，有 证明思路：称为随机向量的二次型，由于 注意到 因此

第三章：回归参数的估计

★★★ 3.1 OLS：回归系数

OLS的原理是使残差平方和最小，因此在列满秩的情况下有损失函数，容易看出是一个凸函数，因此具有唯一的全局最优解，于是令对偏导为 注意到与都是实数且有，因此当可逆时，有 在此我们得到了的解析解，称为帽子矩阵，记为；称为Annihilator矩阵（消灭矩阵），二者可以视为对的线性变换，分别将映射到观测向量空间与残差向量空间。对于而言，有 而且与还是互相正交的（欧氏空间意义下）， 实质上这是与均为对称幂等阵的原因，或者说作为线性变换与将映射为两个互相正交的向量。

此外，从式能看出，，即 ；在后文中我们将证明这个式子。

考虑到很多情况下行空间与列空间维数可能较大，造成计算中的维数灾难，这时解析解的求解不易，通常我们从最“原始”的问题——一个理想的估计应使RSS最小，并通过优化方法求数值解这个问题，即 得益于最小化问题是一个凸优化问题，因此局部最优解等价于全局最优解，我们可以用许多适用于凸优化的算法迭代求解。尽管解析解在理论推导中举足轻重，很“精确”也很漂亮，但实际应用中，解析解是没有必要的而且需要大量的算力（主要体现在求高维矩阵的逆），所以更多的是通过上式利用优化函数求数值解。

通常用MSE评价估计的优劣，对于OLS而言，有 可以看出，OLS的MSE可以被分解为回归系数估计的方差之和与偏差平方和。

值得一提的是，尽管我们求OLS的出发点是使RSS最小，但在推导过程中可以特别导出OLS的另一个性质：使得残差之和为，或者等价地说残差的样本均值为。证明这个性质只需要将前文中损失函数对的偏导改为对的偏导（实际上，从这里我们可以知道这个性质是极其自然的，源自于我们推导OLS中所设的）：首先需要明确由最小二乘原理，可以得到 又注意到，于是 得到最终的式子 最后，我们联合上文已证明的与互相正交，可以总结出： 对于需要预测的新数据集，预测值的解析解​.

注：当误差独立同分布时，截距项与回归系数的OLS与广义矩法估计等价，均为。

★★ 3.2 高斯-马尔可夫定理

在大前提条件

• 对回归系数是线性的，即要求回归参数均为常数，以后简称为线性假定；

• 样本必须是以某种方式随机抽样得到的，且不应存在严格多重共线性；

下，若还有

• 弱外生性（零均值）：；

• 球形扰动项 1（同方差）：；

• 球形扰动项 2（不相关、不存在自相关）：.

则有

  1). 无偏性与可计算的协方差阵：，且；

  2). 线性无偏估计：由于是的线性变换，再加(1)因此是线性无偏估计；

  3). BLUE：是所有的线性无偏估计里方差最小的，是最佳线性无偏估计.

注：由严格外生性可以导出弱外生性。

证明思路：利用与，于是可证无偏性 对于估计的协方差阵，利用上文证明的无偏性与高斯-马尔可夫定理条件，于是可证 只需要注意到在最后一步中一定是对称正定矩阵，有​。

3.3 稳健标准误

标准差是用以衡量总体离散情况的，而标准误是用以衡量样某样本均值有效性的，即这个样本均值的方差。针对不同的问题，选用相应的标准误，是求出OLS在不太理想情况下真实标准误的办法之一（所以叫“稳健”）。

如果数据存在一定的多重共线性或自相关性，且坚持应用线性回归模型，则可考虑更换标准误、更改模型GLS或进行准差分。

① 值得一提的是，证明中导出了，在高斯-马尔可夫定理条件下进一步导出的最终结果是我们进行估计参数的显著性检验的基础，这时认为，称为的同方差稳健标准误。

② 当不尽相同但间无关，假设时由于不满足，这时便没有了，导致原先的t检验、F检验都会失效，若仍打算采用OLS作为我们的估计且需要对估计参数进行显著性检验，在随机误差间无关的条件仍成立下可以用代替，于是可以得到，这样有了理论上的我们才得以进行后续的分析，并称为为的异方差稳健标准误，对于t检验、F检验等一众假设检验，只需要将同方差稳健标准误替换为异方差标准误便能继续进行。

③ 与此同时，要注意到这只是针对OLS导出的概念，对于WLS并不适用，记WLS的权重矩阵为，则 当取权重矩阵为，即主对角线第项皆为，这时，我们能得到WLS各系数估计在理论上的准确的方差，可以看出异方差稳健标准误对于WLS是没有什么意义的。实质上WLS可以说就是为“异方差”但“不相关”问题而生，Alexander Aitken证明了对于“异方差”但“不相关”问题WLS才是BLUE，而不是OLS。针对WLS，我们有White稳健标准误，他的取值为，替代OLS的多种检验中的同方差标准误以达到对估计参数进行显著性检验的目的。

④ 当不尽相同且随机误差间相关性与类相关，同类的与不相关，不同类的与无关，这时需要进一步用到聚类稳健标准误的概念，直观上看是针对不同的类分别求异方差稳健标准误，如此一来我们可以把异方差稳健标准误的概念推广到聚类稳健标准误来。

⑤ 如果不仅不尽相同，而且任意随机误差之间都是相关的（或相关性无法判断，也是任意的），这时并没有“一个万能的稳健标准误”，自然也没有什么好办法进行OLS参数估计的显著性检验。

★★ 3.4 OLS：σ²

当满足高斯-马尔可夫定理的前四个条件时，是的一个无偏估计。也就是说，即使不满足高斯-马尔可夫定理的第五个条件，也是的无偏估计；只不过，当条件时，进一步有，而这在前文中是已证明的。

证明思路：对于无偏性，只需要说明为什么RSS除自由度后使得同的OLS一样具有无偏性；首先证明与帽子矩阵的一些性质，注意到，即是对称阵，而且还是幂等的 于是 有了RSS解析式与帽子矩阵的性质，注意到前文中我们推导的随机向量二次型期望公式——与对称阵，皆有，同时需要强调的是我们这里把视为一个服从模型分布的随机变量，所以 综上所述，这时有 这里需要观察到，所以 至此证明了当满足高斯-马尔可夫定理的前四个条件时是的无偏估计。

3.5 正态假设下的OLS

◆ 3.5.1 回归系数与σ²的分布

由前文的推导，容易知道：

• 当误差独立服从零均值的正态分布时，与OLS相同，且；

• 这时的MLE为，这是一个有偏估计；

• ；

• 在模型线性关系不显著的条件下，；

• ​与RSS独立；

• 估计在Cramér–Rao下界的意义下是渐进有效的。

这为最小二乘法提供了一个非常“传统统计”的解释（即不考虑历史因素，为什么最小二乘法比最小一乘法更常见）：在满足高斯-马尔可夫定理条件时，若误差还独立同分布于零均值的正态分布，则此刻OLS等价于MLE，这时回归系数的最小二乘估计正是极大似然估计。

当不确定误差的分布或误差不服从正态分布时，一般也会优先考虑OLS而非MLE，因为MLE的数值优化常常是非凸的，优化问题会棘手一些。

3.5.2 置信区间与预测区间

在高斯-马尔可夫定理成立、误差服从正态分布与的置信水平下，若记为矩阵的第行第列的值、为帽子矩阵的第行第列的值、，则：

的置信区间为 的置信区间为

的置信区间为 的预测区间为 预测区间较之置信区间会更宽一点。

当样本量较大且模型合理时，帽子矩阵近似为，即近似于，所以有的近似预测区间为 以上估计区间构造的前提条件均为未知。如果已知，则将分布改为正态分布、将替换为后，可以得到更精确的估计区间。

library(ggplot2)

data(diamonds)
df <- diamonds[1:20,]

model <- lm(price ~ carat, data = df)

p <- ggplot(data = df, aes(x = carat, y = price)) +
    geom_ribbon(aes(ymin = predict(model, newdata = df, interval = "confidence")[,2], ymax = predict(model, newdata = df, interval = "confidence")[,3], fill = "Confidence"), alpha = 0.5) +
    geom_ribbon(aes(ymin = predict(model, newdata = df, interval = "prediction")[,2], ymax = predict(model, newdata = df, interval = "prediction")[,3], fill = "Prediction"), alpha = 0.2) +
    geom_line(aes(y = predict(model)), color = "#1E90FF", linewidth = 0.8) +
    labs(title = "Linear Regression of Price on Carat", x = "Carat", y = "Price (US Dollars)") +
    geom_point(alpha = 0.8) +
    theme_bw() +
    theme(
        plot.title = element_text(size = 14, face = "bold"),
        axis.title.x = element_text(size = 12),
        axis.title.y = element_text(size = 12),
        panel.grid.major.x = element_blank(),
        panel.grid.minor.x = element_blank(),
        panel.grid.major.y = element_line(color = "grey80"),
        panel.grid.minor.y = element_line(color = "grey90"),
        plot.margin = margin(1, 1, 1, 1, "cm")) +
    scale_x_continuous(expand = c(0.01, 0.01)) +
    scale_y_continuous(expand = c(0.01, 0.01)) +
    scale_fill_manual(values = c("Confidence"="lightblue", "Prediction"="lightgreen"), name="Interval")

plot(p)
# ggsave("interval.svg", plot = p)

将置信区间和预测区间可视化：

为什么预测区间要比置信区间更宽呢？在回归模型中，误差通常包括两个方面：不可以减少的误差（偏差）和可以减少的误差（方差），预测区间衡量的模型参数完美存在的不可以减少的误差还衡量可以通过回归减少的误差，而置信区间仅仅衡量了可以减少的误差。

3.5.3 参数的显著性检验

用以推断是否可以认为参数为的假设检验，如果检验的p-value很低，说明这些参数显著地不为，是有效的，那么理论上就不应从模型中删掉这些变量，起码与这些参数们理应有较明显的线性关系。当然，这是比较传统的方法，历史上曾通过逐步回归（从无开始，逐步增加参数个数并做显著性检验，排除未通过者；或反之，从考虑所有的参数开始，逐步减少参数个数）来确定参数的选择，个人认为在大数据与计算机的时代，应该直接以优化的目标函数为最终目的，只要加上某参数能使得RSS明显降低，那么就不应该将其删除。注意，由于潜在的多重共线性，完全可能当两个变量同时存在时RSS值较大，但删去其中一个变量后RSS显著降低。

要注意，除了显著性，还要考虑检验的势（power）；因此，如果p-value，则只能得出不能拒绝原假设的结论，但这不代表就要接受原假设——这是很基础的内容，不再赘述。可以参考《Scientific method: Statistical errors》，由Regina Nuzzo于2014年发表于《Nature》。

参考链接：Scientific method: Statistical errors

中文翻译版本（果壳译）：统计学里“P”的故事：蚊子、皇帝的新衣和不育的风流才子

𝑭检验

F检验是对模型整体显著性的检验，有别于t检验仅仅是针对单个回归系数的检验。对一元线性回归而言，二者等价。

• ：；

• ：.

则在成立的条件下，有 其中为模型实质上的残差平方和，为在原假设成立情况下的“预设”模型的残差平方和，很显然，当原假设接近“真”时，二者差距应该较小，这时统计量的值较小，所以拒绝域为，p-value为。如果检验的结果表明线性关系显著，即检验的p-value小于显著性水平或统计量的值落入拒绝域，则拒绝，认为模型整体上的线性关系成立，也就是至少有一个自变量与因变量之间的线性关系显著。

前文已经证明，当高斯-马尔可夫定理的条件成立时有，那么统计量的导出就十分显然了。统计量通常被用来检验两正态分布的均值是否相等，实质上利用的是两个样本集合的方差估计值构造统计量进行假设检验，这正是方差分析的思想。

这里的检验统计量也在承担一个类似方差分析的中检验统计量的角色，因为在高斯-马尔可夫定理的条件成立时有，于是分母服从分布；再结合线性模型的可加减性易知分子服从分布，这就是检验统计量的构造思想和推导过程。

有趣的是，容易证明总是存在（这有一个很通俗的解释，但也可以严谨地证明，读者不妨一试）。

最后，检验中假设为的参数们可以根据需要进行调整，如果有个值被假定为，只需要将替换为即可；另外，也能够对进行检验，这等价于检验。

𝒕检验

t检验是对单个回归系数显著性的检验，有别于针对模型整体显著性的F检验。对一元线性回归而言，二者等价。

• ：；

• ：.

则在成立的条件下，有 其中是的标准误估计，该公式的含义是“标准化为t分布”，因为在高斯-马尔可夫条件与皆成立时有（枢轴变量），消除了量纲的影响；当分母为标准差时，在高斯-马尔可夫条件下检验统计量应该服从标准正态分布，又由于分母本身是一个服从的估计，故根据分布的定义，的自由度为。检验的拒绝域为，p-value为。如果检验的结果表明p-value小于显著性水平或统计量的值落入拒绝域，则拒绝，认为被检验的回归系数的自变量与因变量之间的线性关系显著。

对一元线性回归而言，检验等价于检验（毕竟在只有一个回归系数的情况下，对回归系数做检验和对模型本身的线性关系做检验没有区别），检验统计量的平方即为检验统计量 （这也符合同分布于的特征）。

更进一步地，检验也可以用以检验的假设，只需要等价地检验即可，这实质上是构造了统计量。

当模型明显不满足高斯-马尔可夫定理的条件，如存在严重的多重共线性时，检验将不再可用，而检验在加以改造后却仍有效：可以将替换为其他可用的稳健标准误估计，检验便可以继续执行。

最后，我想简单阐述一下，p-value很小不代表该回归系数能正确反应真实模型。

library(ggplot2)
library(svglite)

set.seed(123)
x1 <- rnorm(50)
y1 <- 2 + 3 * x1 + rnorm(50)
set.seed(321)
x2 <- rnorm(50)
y2 <- 8 + 3 * x2 + rnorm(50)
data <- data.frame(x = c(x1, x2), y = c(y1, y2), group = factor(rep(c("A", "B"), each = 50)))

g <- ggplot(data, aes(x = x, y = y)) +
    geom_point(aes(color = group, shape = group)) +
    geom_smooth(
        formula = 'y ~ x',
        method = "lm",
        se = FALSE,
        aes(color = group)
    ) +
    # scale_color_npg(palette="nrc") +
    scale_color_manual(values = c("#D4B9F0", "#A8C000")) +    # Lavender: #D4B9F0
    theme_bw() +
    labs(
        title = "Linear Regression",
        x = "X",
        y = "y"
    ) +
    geom_smooth(
        formula = 'y ~ x',
        method = "lm",
        se = FALSE,
        color = "#A52A2A"
    )

plot(g)
# ggsave("Linear_Regression.svg", plot = g)

可视化结果如下：

进行显著性检验：

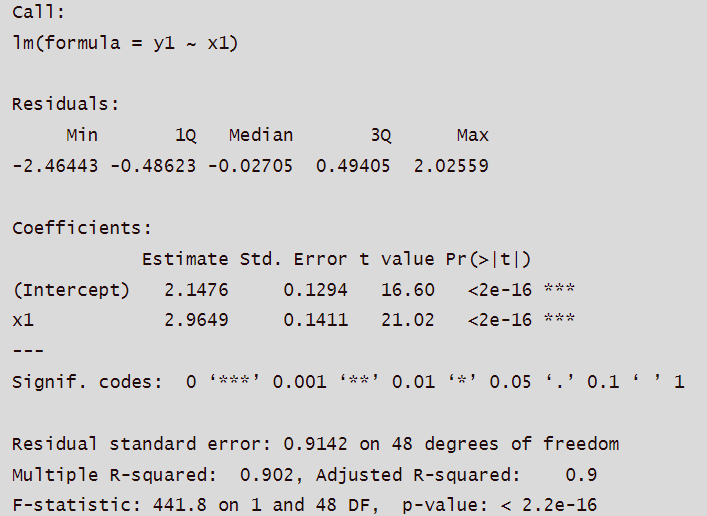
summary(lm(y~x, data))

结果表明回归系数高度显著，但显然的是这个模型从最初的假设开始就是错误的（关于结果解读见下文）。所以，只根据显著性检验结果完全地判断模型好坏与决定参数筛选是不合理的行为，有些时候即使某个回归系数没有通过显著性检验，但它能使RSS大幅降低，那么它亦是应该被保留的。

这些检验统计量的构造背后的统计思想非常有趣，环环相扣、精彩绝伦。

3.6 中心化模型与标准化模型

3.6.1 中心化模型

由于通常我们只关心回归系数的值，下面将证明这种情况下将模型中心化是可取的操作。

设原本的回归模型为，即，现将设计矩阵与其第一列分离，转写为，其中 记中心化后为，有

为保证与不变，令，于是得到中心化模型 这仍然是个线性模型，且若原本的回归模型满足高斯-马尔可夫定理条件，容易知道中心化后的模型仍满足高斯-马尔可夫定理条件，这使得模型中心化后依然有各种优良的统计性质，不难导出中心化模型的OLS： 、分别是、的无偏估计，注意到，后续不难得到 若进一步有随机误差，则根据正态分布的性质，不仅有、，而且与还是独立的。

3.5.2 标准化模型

唯一值得指出的是若在基础上进一步进行标准化，记我们得到的新矩阵为，不难证明，其中是不考虑第一列的相关阵。

★ 3.7 拟合优度𝑹²与调整的拟合优度

SSE与RSS都表示残差平方和，只是记号不同，SSR则代表回归平方和。SSR反映了SST中由于与的线性关系而引起变化的部分，是回归模型可以解释的部分；SSE是与除了线性关系外、由其他因素引起变化的部分，是模型不能解释的部分。易见的取值范围为。

由此可见，模型越贴切样本，则由导致的SSR占比总偏差SST中的部分就应该较多，或者等价地说，预测值与真实值偏差平方和SSE占比总偏差SST应该较少，那么就越趋向，所以理论上拟合优度越大便说明模型对样本集的拟合就越好。

同时，也应注意到当参数越多，即使增加的参数并不能很好的解释模型，但更多信息的加入总是不可避免得会使得模型拟合更“优”、SSR占比SST越大，例如将某人一天的碳排放量作为一天全球碳排放量的解释变量，而这就是过拟合的情况，不仅弱化了模型的泛化能力，还使得模型难以解释。造成这种情况的原因是只考虑了针对特定样本集的信息，所以如果只以为模型的唯一评价指标，则会倾向对于模型选择更多的对因变量影响极小甚至是出于样本的偶然因素才“看上去和因变量有关”的自变量，可能导致严重的过拟合问题与多重共线性，模型的解释性也大幅降低。

因此提出了调整后的拟合优度：

不仅考虑到了SSE与SST的关系，也考虑到了不宜过多的参数个数，在二者之间做了权衡。从公式中可以看出一定小于，而且甚至有可能取到负数。实际上，在现实应用场景下，比更为常见。

▲▲▲ 3.8 模型解读

语言原生的线性回归模型，以下图为例

有必要解释一下图中在“Residual standard error”注释中“参数个数”的意思：暂只考虑向量代表一组无序的名义数据的情况，例如我们所选取的“class”自变量，它包含了种树的种类，作为分类数据（属性数据）在回归中我们需要用一个具有七种取值的向量分别对应这七个类别，这时分量个数通常选择六或七个。如若选用六个分量构造，则取七个向量作为所有可能的且不同的取值，一般选择、、、、（必须注意到，虽然我们一共仅使用了六个分量，却用六个分量表示了七个线性无关的向量，这实际上对应了七个品种），记，则，且中至多有一个值取（再次强调，只能有七种不同的取值）；此时回归模型为： 模型中我们有个自变量与回归系数，但自由度却并不为：由于我们在回归中实质上使用到了样本均值，故残差标准误自由度为（也可以认为亦“占用”了一个自由度）；当然还可以用七个变量表示七种种类，记，取所有可能的取值为、、、即可。

再考虑“displ”自变量，这是一个连续取值的自变量，是一个实际数据，因此用一个随机变量表示即可，此时回归模型为： 其中，当，且至多有一个分量取，而理论上可能取到任何非负值（当然在这个问题中它具有现实意义，取值有一个范围），这时残差标准误自由度为。因此，“参数个数”指模型回归系数与截距项个数之和，等价于模型自变量个数加。

---

题外话：对于有序的名义数据，仍然可以只使用一个变量表示，譬如考虑调查者的学历水平，取小学及以下学历，初中学历，高中学历，并以此类推。那么，为什么在刚才的例子中“class”自变量我们使用了一个六维向量来表示，而不是只是用一个标量，令其取值分别为、、、来表示“class”的这七种种类呢？

答案是学历水平在简单实验中可以粗糙地认为是有序数据，而树的种类必然是无序的、线性无关的，否则会出现“用表示树的种类，对樱桃树取，对柠檬树取，所以柠檬树的种类是樱桃树的两倍”这样错误且荒谬的推论。

▲▲▲ 3.9 CLS（线性约束的最小二乘估计）

考试时会给出公式。

设有线性约束，则利用Lagrange乘子法可以导出线性约束下的最小二乘估计：

★★ 3.10 残差向量的性质

若满足高斯-马尔可夫定理的假设，则

  (1). ；

  (2). ；

若随机误差还服从正态分布，，则

  (3).

◆◆ 3.11 回归诊断

不涉及绘图的考察，但考察解读。

library(tidyverse)
library(tidymodels)
library(performance)

# use data "MPG"
fit <- linear_reg() %>%
set_engine("lm") %>%
fit(hwy ~ displ + class, data = mpg)
check_model(fit)

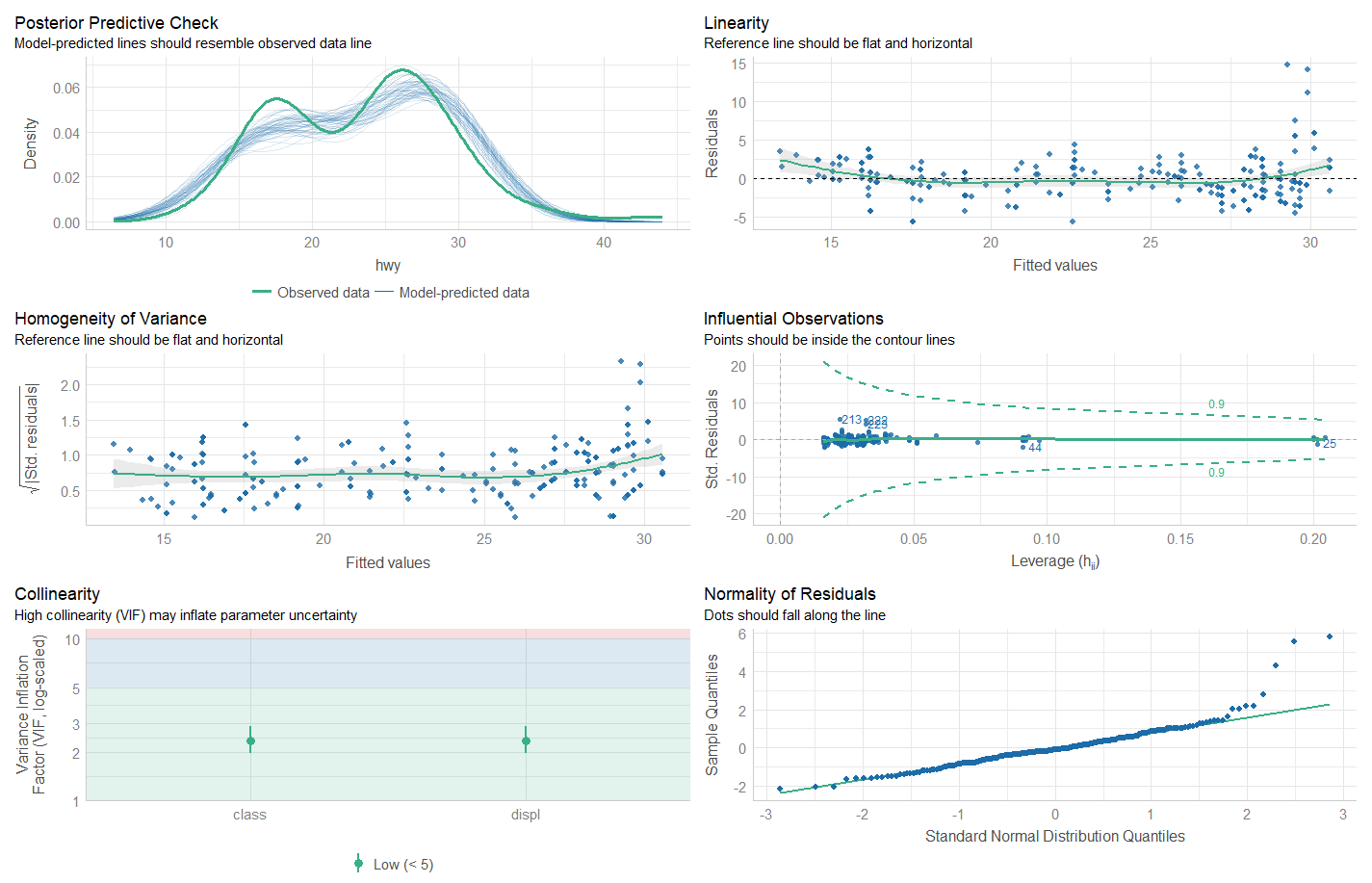
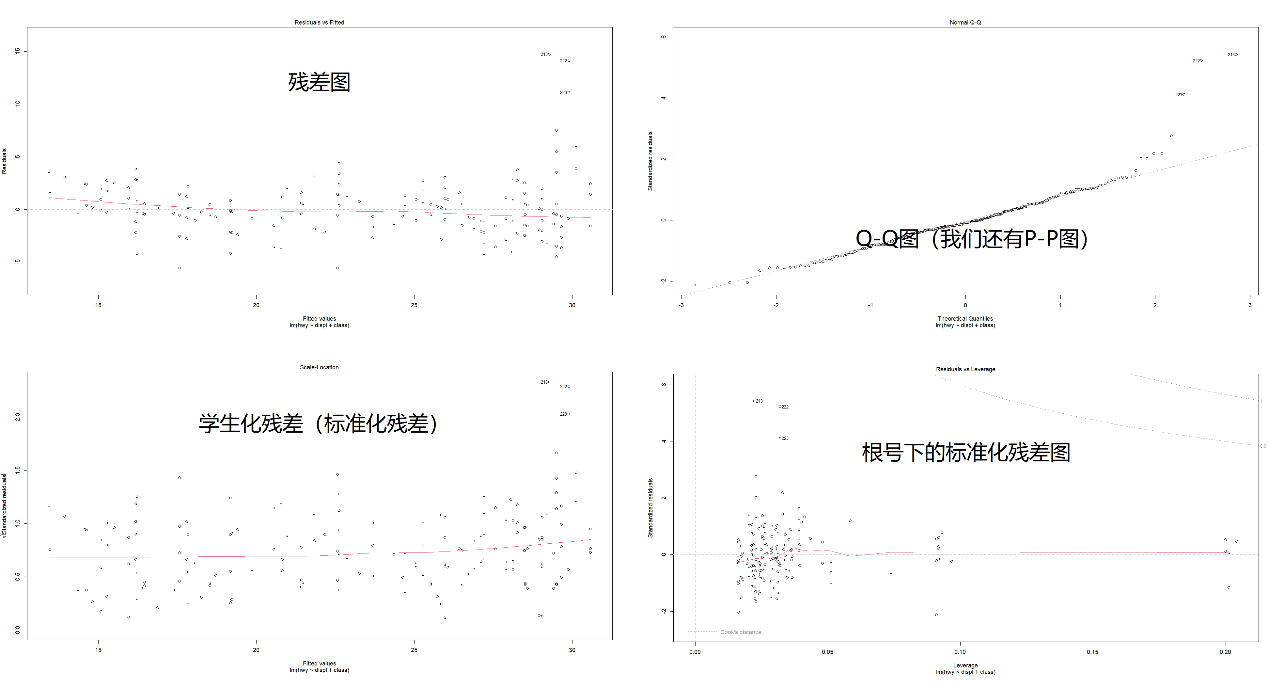
学生化残差图、Q-Q图等图像均可用于初步判断数据正态性、峰度、偏度与趋势。需要说明的是，Q-Q图的斜率为标准差、截距为均值。

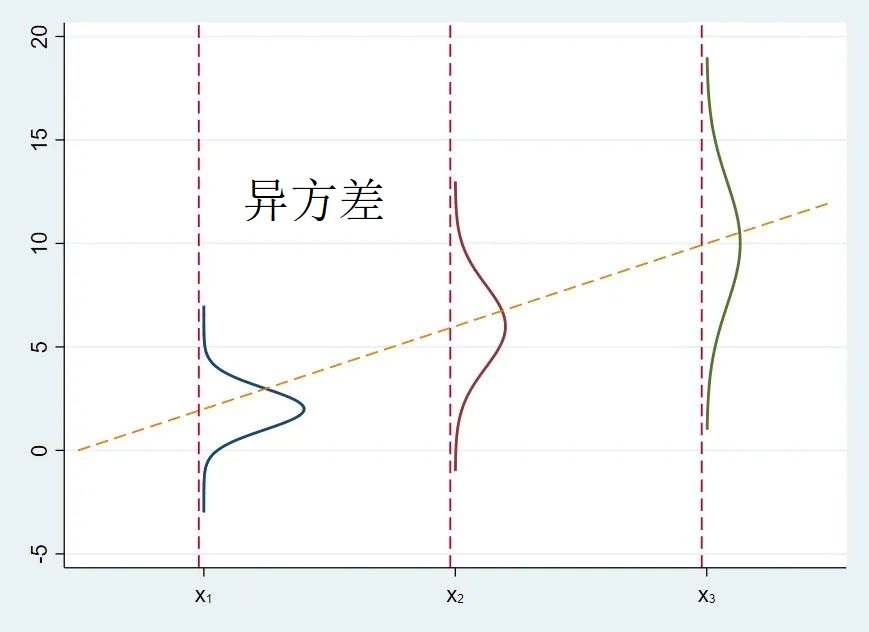
◆◆ 3.11.1 异方差问题

名词解释，要求作图并加以描述：说明是异方差问题？即不满足“同方差”假设，这种情况非常普遍，常常发生在截面数据，如消费对收入的回归、成绩对学习时长的回归，通常认为异方差源于，随机误差的方差与自变量间存在线性或非线性的关系，即

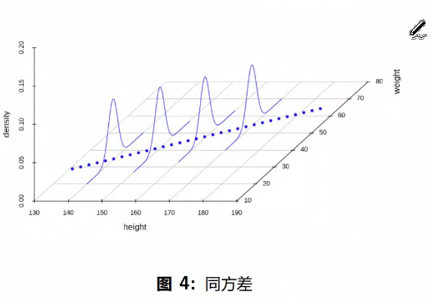
异方差不会影响的：

  (1). 不改变OLS的无偏性，仍是无偏估计.

异方差会影响的：

  (2). OLS有效性大大降低，系数估计的方差大大增加，导致预测的精度降低；

  (3). 多种对系数估计的显著性检验失效，譬如t检验、F检验.

值得一提的是，对于问题(3)可以改检验中的标准误为异方差稳健标准误以继续进行假设检验，但对于问题(2)，Alexander Aitken证明了这时BLUE应是WLS而非OLS。

继续减弱条件至不同的随机误差间可能相关，但我们提前知道样本点的随机误差间的相关阵，则这时GLS才是的BLUE，因此可以说WLS是OLS的推广，GLS是WLS的推广，三者对于“同方差”、“不相关”的依赖在逐渐递减，但后者可能不太实用，因为估计一个矩阵以今天的方法和算力都是极其困难的。

通过画-图加以说明“异方差”的表现，如

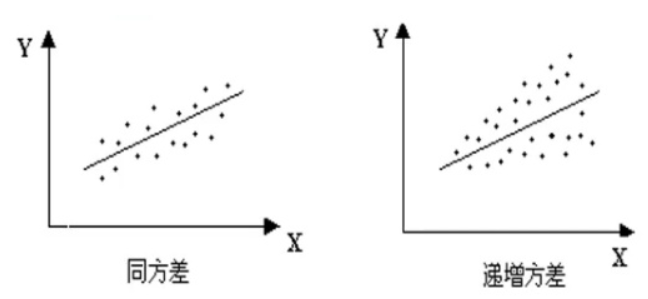
◆ 3.11.2 残差图与学生化残差图

不考察学生化残差图。

在高斯-马尔可夫定理条件下与独立，因此以为横坐标、为纵坐标的散点图应不会呈现任何趋势，称这个散点图为残差图。

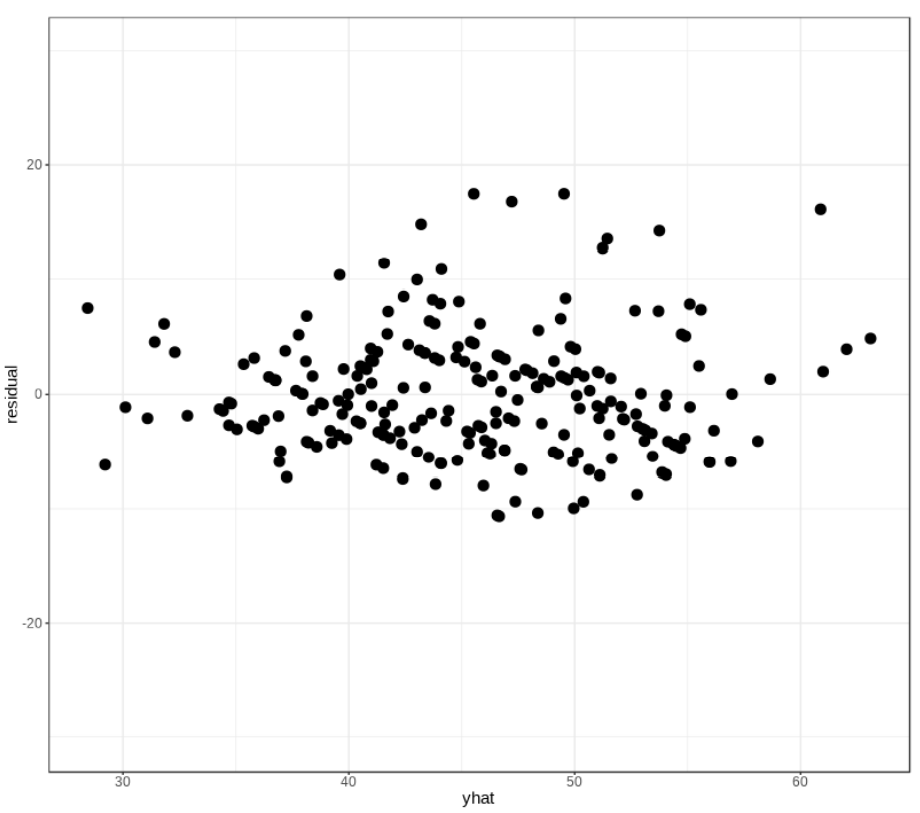
如果存在异方差，则图像应有明显趋势

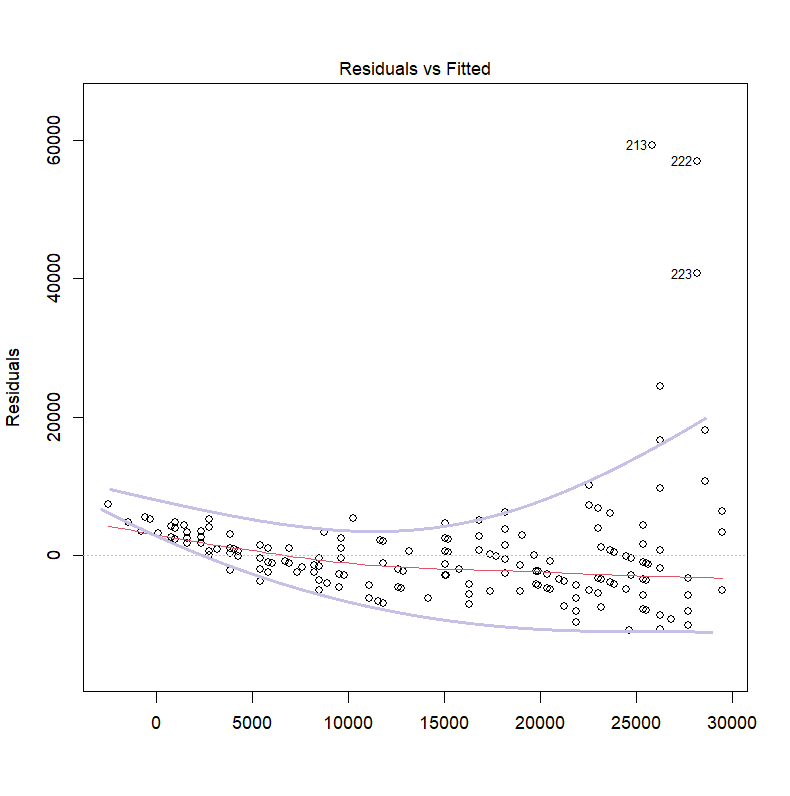
◆ 3.11.3 Breusch-Pagan检验

Breusch-Pagan检验简称BP检验，由Trevor Breusch和Adrian Pagan于1979 年提出，原理是对每个可能的进行方差分析（线性回归），构造如下辅助回归方程 的含义是不可或未观测项，通常包含了模型的随机误差，可能与无关，也可能代表与间的非线性关系。

原假设为，检验原理是在原假设成立时 或由拉格朗日乘子等价地导出 一般在不能拒绝原假设（值较大）时，可以认为原回归模型满足“同方差”假设。

注意到如果拒绝原假设，则一定有“异方差”存在，但由于BP检验所假设的辅助模型是一次线性回归（特殊的线性回归，方差分析），这只能表明原模型必然不满足“同方差”假设，而不能说明与间一定存在某个线性关系。

library(lmtest)

fit <- lm(hwy ~ displ + class, data = mpg)
bptest(fit)

譬如上图的结果，由于，因此没有的把握拒绝原假设，模型可能是满足“同方差”假设的。

◆ 3.11.4 White检验

White检验可以认为是“BP检验 Plus”，原理是对每个可能的进行二次回归并考虑交叉项（自由度过小的话我们常常去掉交叉项），构造如下辅助回归方程 原假设为，检验原理为在原假设成立时 一般在不能拒绝原假设（值较大）时，可以认为原回归模型满足“同方差”假设。

注意到如果拒绝原假设，不能说明方差与自变量间一定具有二次关系，因为White检验假设的模型是二次回归，方差与自变量有可能是高次关系或其他非线性关系，这只能表明必然不满足同方差假设，这和BP检验相似。

◆ 3.12 Cook距离与强影响点（异常点）

强影响点：对模型回归结果有较大影响的样本点，如果不考虑该点会显著改变经验回归方程，即Cook距离较大的点。

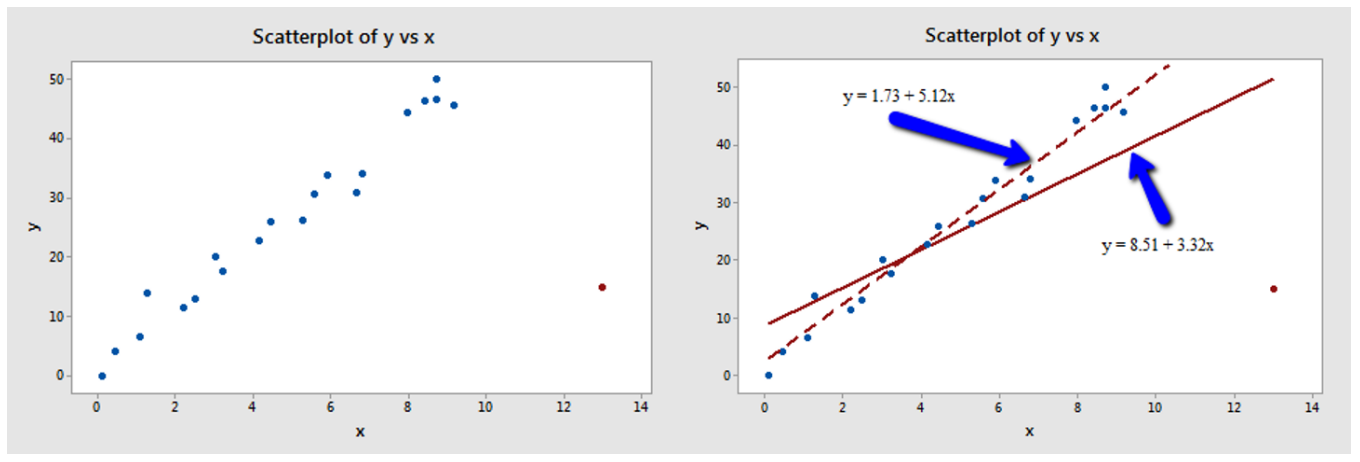
Cook距离：记考虑全部的样本点进行回归，得到的参数的OLS为，对某一样本点记为，去掉该样本点考虑剩下的样本点进行回归，得到的参数的OLS为，称为的Cook距离：

◆ 3.13 Box-Cox变换

只考察名词解释。

单参数的Box-Cox是对因变量的变换，定义为 常用的Box-Cox变换有、与，注意Box-Cox变换直接作用于因变量。尤其是时常被用到，这是因为如此操作，系数仍可以有良好的解释（见上文），也缩小了极端大值与较小值的差异。

对于右偏分布，取对数通常能让数据更加正态。

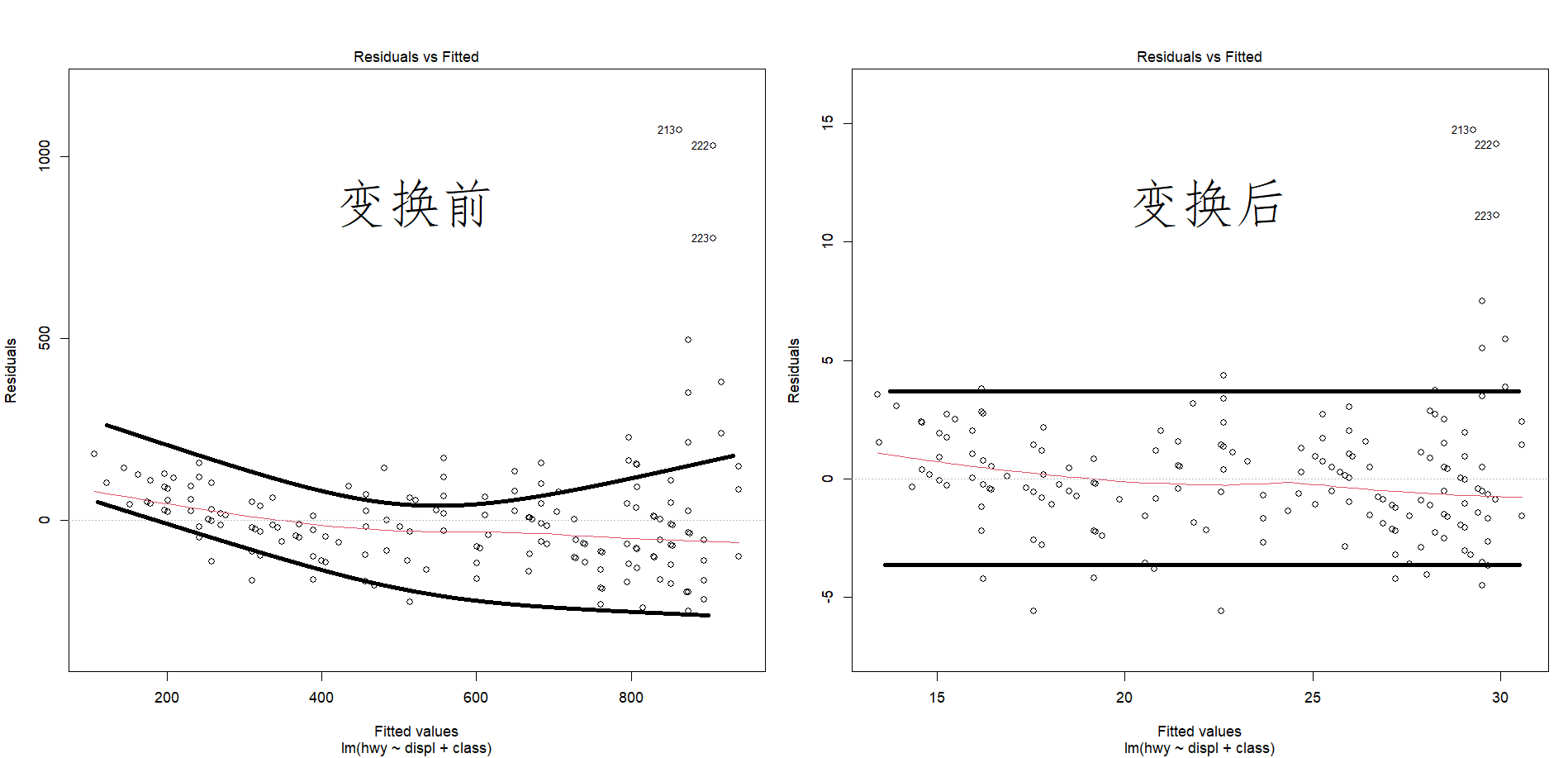
双参数的Box-Cox变换为：

★★ 3.14 多重共线性

如果存在多重共线性，可以直接删掉强线性相关的一些变量或采取后文逐步回归的方法，但这样做并不“优雅”；此时可以考虑一些线性降维手段，例如PCA，或是采用带有正则化项的回归算法，例如岭回归、Lasso回归甚至一些非线性方法等。

★★ 3.14.1 多重共线性的名词解释

名词解释：多重共线性指模型自变量之间存在近似的线性关系，例如 在这个例子中，“研发费用”、“宣传费用”与“总投入费用”之间便可能存在较强的复共线性关系，严格成立 可能带来的影响有：

 ① 设计矩阵不列满秩；

 ② OLS的方差过大，参数的置信区间过大；

 ③ 显著性检验（F检验、t检验）失去意义；

 ④ 回归系数的平均长度远大于实际长度，并可能伴随符号与现实意义相背离；

 ⑤ 结合以上几点，导致模型的预测失效。

其中第 ④ 点将在后文“特征根判别法”中作推导。

3.14.2 题外话：最小二乘估计家族

高斯-马尔可夫定理条件下OLS是最优无偏估计，但高斯-马尔可夫定理条件通常过强：

削减“同方差”我们可以从OLS导出WLS，再削减“不相关”我们可以从WLS导出GLS。

削减“解释变量的样本有波动，即没有自变量是常数，也没有自变量之间具有完全共线性”，可以导出岭估计、Lasso估计与Elastic Net回归等多种OLS的推广。

这样看来，数学家和统计学家在做的事就是基于已有的东西，想法设法让今天的“推广”变成明天条件更弱情况下的“特例”。

◆ 3.14.3 特征根判别法

特征根判别法的推导过程对理解线性回归非常重要，甚至可以由此引出岭回归、Lasso回归。

首先假设设计矩阵列满秩，记为不含第一列且已标准化的设计矩阵，这时便是自变量的样本相关阵，由此可以看出两两自变量之间的线性关系；若要考察多个自变量间的线性关系，理论上“多个自变量间具有相关性”与“存在较小的特征值”等价。

设的特征值为（是正定阵），记第个特征值对应的特征向量为，如果存在一个接近于的特征值，则 由此可以导出，如果存在多重共线性，与表现出强烈的列相关。因此可以用最大特征值比最小特征值，即来初步衡量共线性，经验上认为若则认为存在一定的共线性，则认为共线性极强。

基于此，可以进一步说明为何多重共线性会导致OLS偏大，记为标准化模型的OLS，也就是消除了量纲影响的OLS，又由于是正定矩阵，所以一定存在维正交矩阵使得，于是有 由于存在多重共线性时较小，由上文的推导知此时相距会有一个很大的偏差，这就是为什么多重共线性会导致估计值异常大。

◆ 3.14.4 VIF检验

同样地，本文作为课程复习不做详细推导，在此只说明原理。

原理：将每个对剩余的个自变量建立回归模型 使用OLS估计参数，记作因变量回归模型的拟合优度为，称为的方差膨胀因子。

容易看出，如果较大说明自变量间的线性关系的确存在，等价于较大，因此经验上认为则存在较强的复共线性；自变量较多时，认为则存在较强的复共线性。

3.15 逐步回归

★★ 3.16 WLS（加权最小二乘估计）

★★ 3.16.1 一般的WLS

称为WLS。作为OLS的一种改进，WLS是针对异方差情况而提出的，弱化了OLS要求同方差的条件。

注意，通常取WLS的权重矩阵为对角阵的逆，这里对二者不加区分。

WLS通过加权损失函数导出，其步骤与OLS的推导相同。

实质是经加权的RSS，可以等价地写作。

▲▲▲ 3.16.2 分组的WLS

◆ 3.17 GLS（广义最小二乘估计）

只考察GLS性质的掌握。

此外还有FGLS，即“可行广义最小二乘估计”，可以参考：

• mathworks: FGLS
• Wiki: Generalized_least_squares

3.17.1 GLS性质

当、且是模型的GLS，则

  (1). 是无偏估计，；

  (2). ；

  (3). ，是的BLUE.

记OLS为，则任何情况下都有。

3.17.2 GLS的导出

思路是将对角化再运用OLS。设且正定并已知，记，，，则有 因此可以得到OLS：，对于模型与模型参数，具有高斯-马尔可夫定理条件下一切性质，再者 于是对于模型与模型的参数也是无偏的，且。

★ 3.18 岭回归

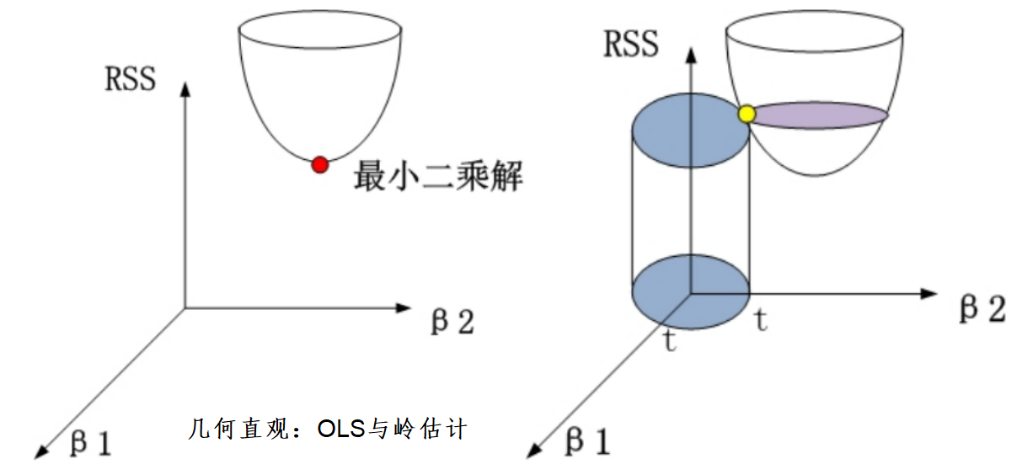
3.18.1 岭回归的性质

岭回归由Hoerl和Kennard于1970年首次提出，考试可能考察岭估计的推导。

前文“特征根判别法”有推导到，在多重共线性的影响下OLS可能异常的大： 因此岭估计的初衷就是限制估计的长度，这就是为什么说岭估计是带有范数约束的最小二乘估计，因为岭估计通过在损失中加入正则化来均衡取舍残差平方和的最小化与正常范围的估计长度；类似的Lasso回归采取了正则化。下文给出的岭回归损失函数中，岭参数就是长度的的权重：越大，对损失贡献越大，对异常长度的惩罚越大，得到的岭估计与OLS的差值越大。

岭估计证明思路：从岭回归（Ridge Regression）模型出发， 其广义拉格朗日函数为（这就是他的损失函数），当可逆时令对偏导为，

至多考察验证岭估计为何有偏。

证明思路：已知岭估计的解析解为，在高斯-马尔可夫定理中随机误差的“零均值”、“同方差”、“不相关”假设下有，则

我们知道，任何一个可逆方阵的逆是唯一的，既然的逆是，那么对于，一定有，否则。因此，必然不是的逆，然而当且仅当左乘其逆时结果为单位阵，也只有此时有 所以，对于任何非零的，必定有成立，即：岭估计一定是有偏估计。

进一步地，有 岭估计还有一些性质，读者可以自行证明：

• ，使得岭估计的MSE小于OLS的MSE；
• 岭估计是一种压缩估计，，岭估计的长度均小于OLS的长度；

---

题外话：关于逆矩阵的唯一性，既可以说明，容易知道、由唯一确定，也可以假设、都是的逆，必有，这本应该是无需多言的。

◆ 3.18.2 岭迹法

只考察原理。

  (1). 检验是否存在复共线性；

  (2). 作岭图，对每个回归系数在尽可能小的前提下找到一个使得岭迹稳定的.

选择适合的的标准：

  1. 保证岭大体稳定，不会随增大而显著变化，并且符号合理；

  2. 在保证1.的前提下尽量选取较小的.

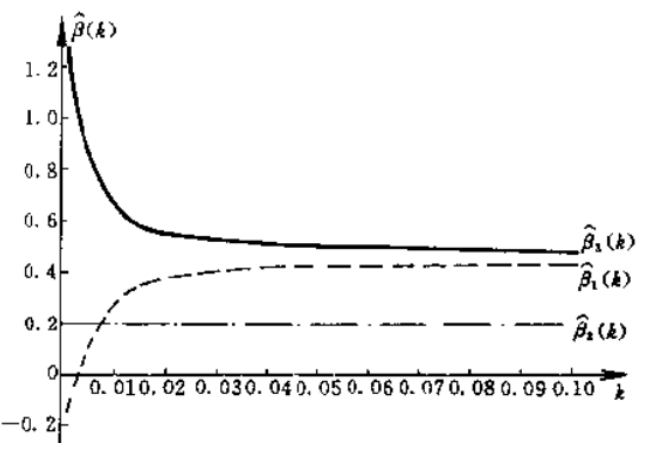
3.18.3 确定岭参数其他方法

有没有一个通用的分析方法，使得我们总能确定岭估计的最适参数、找到那个最合适的而使得岭估计最“优”呢？

事实上，直到今天，人们都没有找到一个通用的办法。岭迹法也只是一个经验法则。但除了岭迹法，统计学家还提出了一些其他的经验法则：

• Hoerl-Kennard公式

  该公式于1970年被首次提出，设为标准化模型的最小二乘估计，提倡用或作为的参数值。

• VIF法

  由得出，与呈反比例关系，所以可以考虑选择一个合适使得所有的均小于某一可容忍的常数。常用的经验数字譬如。

• 双公式

★ 3.19 Lasso回归

“岭估计与Lasso估计的关联和区别也是重点”

Lasso估计于1986年被首次提出，1996年Robert Tibshirani独立发现并推广了Lasso回归。 Lasso估计没有解析解，他也是一种压缩估计，损失函数为，即。

范数允许Lasso估计中某一系数为，所以相较于岭估计他可以选择参数。

简单地讲，岭估计通过在OLS基础上添加了回归系数的范数的约束来限制回归系数的平均长度，一定程度上缓轻了多重共线性使得估计平均长度偏大、符号与现实意义背离的问题；由于采用回归系数的范数作约束，这仍是一个连续的凸函数，因此与OLS一样仍可用梯度下降法进行优化；

而Lasso估计通过在OLS基础上添加了回归系数的范数的约束来限制回归系数的平均长度，与岭估计一样减轻了多重共线性带来的糟糕影响，此外由于范数的特点，使得Lasso回归还具有变量选择的功能；不过范数的解析性质较差，梯度下降法不再适用，可以另行考虑坐标下降法、最小角回归等方法优化求解。

Elastic Net回归综合使用了岭回归的正则化与Lasso回归的正则化。

◆ 3.20 PCR（主成分回归）

只考察名词解释。

3.21线性回归的James-Stein estimator

参考另一篇文章：the James-Stein Estimator。

3.22 Bayes观点下的线性回归

在这里我就只做介绍了，这是个非常有趣的观点。但是如果让我做科普性介绍，我仍然会从多重共线性与结构风险、经验风险和正则化惩罚的观点来做解释。

1. 普通线性回归可以通过正态分布及MLE解释（原因与推导在文中有所提及）；
2. 岭回归可以通过正态分布及MAP（最大后验估计）解释，直接推导即可；
3. Lasso回归可以通过Laplace分布及MAP解释.

对于2.、3.在此我就不推导了，直接贴知乎上的回答：

第四章：计量经济学初究

4.1 面板数据

何谓面板数据（panel data）？面板数据是指不同对象在不同时间上的指标数据，在计量经济学和实际生活中广泛存在，与时间序列对立却又互相有着千丝万缕的联系。粗糙地说，面板数据是截面数据的时间序列。把全部数据想象一个面包，面包的长度想象成时间，在面包任意一处切下一片薄片，不同的薄片上的有着一组相同属性的信息，薄片上的纹理孔洞就是一组数据，研究面板数据就是在研究每片面包片上不同的纹理孔洞的关系。

通常，面板数据有如下优点：

• 有助于解决遗漏变量的问题：一般来说，遗漏变量是由个体的差异造成的，若这种差异并不随时间变化而变化，则面板数据是解决此问题的一大利器；
• 提供更多个体动态行为的信息；
• 样本容量较大.

然而，面板数据也有一定的缺点：

• 往往同一个个体不同时刻的扰动自相关；
• 数据获取难度相对较大.

4.2 工具变量（工具变量估计法）

当有变量与模型中随机解释变量高度相关、互为因果（内生），但却不与随机误差项相关，那么就可以用此变量的估计替代模型中内生变量得到一个一致估计量，这个变量就称为工具变量（IV），这种方法就叫工具变量法。换句话说，当感兴趣的的解释变量与误差项相关、互为因果，就会使用工具变量代替内生变量。

面对内生自变量，OLS会产生有偏且不相合的估计值。但是如果有可用的工具变量，则仍然可以获得相合估计。工具变量本身不属于解释方程，但与内生解释变量相关，条件是其他协变量的值。

作为工具变量，要求只能通过工具变量影响被替代变量，必须满足：

• 与所替的内生解释变量高度相关；
• 与随机误差项不相关；
• 与模型中其他解释变量不相关；
• 同一模型中需要引入多个工具变量时，这些工具变量之间不相关.

工具变量的外生性检验可以考虑Sargan检验与Basmann检验。此外，还可用不可识别检验或通过偏判断，关于偏相关的理论可以参考半偏相关、偏相关、R方该变量及偏R方的关系。

下文将提到的2SLS就是一种工具变量法。

在这里通过一个例子，来说明工具变量法估计的用法：对一阶需求方程，有，等式两变同时对工具变量求协方差，有 故而有 欲检验工具变量是否具有外生性，可以考虑过度识别检验，这需要用后文提到的2SLS，所以在2SLS的部分再做讲解。

最后的问题是，如何找到工具变量呢？

  1 step: 列出尽可能多的与内生自变量相关的变量；

  2 step: 剔除上一步找得的变量中与扰动项相关的.

通常来说，可以从以下角度出发寻找第一步中的变量：

• 内生变量的滞后项；
• 自然因素；
• 历史因素；
• 生理因素；
• 外生性政策冲击.

4.3 遗漏变量

存在遗漏变量，且该变量与解释变量不相关，则不影响OLS的相合性；但若该变量与解释变量相关，则此时OLS不再相合。

解决办法：

• 加入尽可能多的控制变量；
• 代理变量法；
• 随机实验、自然实验；
• 工具变量法；
• 使用面板数据.

在这里，需要对比一下核心变量与控制变量。之所以加入控制变量，是为了控制住那些对被解释变量有影响的遗漏变量；即使显著性极强也不能就此做出因果关系的判断。

作为代理变量，必须满足：

• 多余性：仅通过遗漏变量作用于因变量；
• 剩余独立性：遗漏变量中不受代理变量影响的部分，应当与因变量独立.

4.4 内生性问题与2SLS（二阶段最小二乘法）

内生性（endogeneity）问题指模型中存在与误差项（或者说因变量）有相关关系的解释变量，导致高斯-马尔可夫定理假设中的外生性条件得不到满足。个人认为，内生性问题比多重共线性问题更严重、更难处理，也更负面，其中后者是自变量之间具有相关关系。在这里暂不考虑异方差下的内生性问题。

内生性会破坏估计的相合性，除了由自变量测量误差所引起（因变量的测量误差不会导致内生性问题），理论上通常还有以下原因：

• 内生性问题 1：自相关性会导致内生性，自相关性检验可考虑的有BG检验、Box-Pierce检验、LM检验与DW检验；

• 内生性问题 2：若遗漏变量与解释变量相关，则此时OLS不再相合。对变量的筛选可以考虑逐步回归，在R语言中可以通过下述代码分别在AIC与BIC准则下实现逐步回归：

  # dataset "df"
  model = lm(Y~., data=df)
  model_AIC = step(model, trace=F)
  model_BIC = step(model, trace=F, k=log(nrow(df)))

• 内生性问题 3：若自变量与因变量存在双向影响问题，即互为因果。可以考虑二阶段最小二乘法（2SLS），不过这需要一定的样本量。该方法步骤为：预估或采取分析方法判断出内生变量后，第一阶段取个工具变量与外生变量，记为，将他们作为自变量、将内生变量作为因变量进行线性回归得到OLS，即对于内生变量列得到其估计列，其中；第二阶段，用内生变量的估计替代内生变量，再对因变量进行线性回归得到OLS，有。应注意，该方法需要满足阶条件：工具变量与外生变量数目不得少于内生变量数（即2SLS要求不能不可识别，且同方差；若异方差，则考虑GMM），换句话说，不能不可识别。

  如果模型满足同方差条件时且恰好识别，则广义矩估计（GMM）等价于2SLS。

  另外，满足阶条件时，2SLS产生的IV估计是相合的。

利用2SLS，可以进行过度识别检验，这是一种检验工具变量是否具有外生性的方法。原假设为所有的工具变量都外生，对模型 利用2SLS的残差考察工具变量与扰动项的相关性 等价于，在成立的条件下有。

关于过度识别检验更形象、更具象的例子，可以参考：如何理解计量经济学中的「检验过度识别约束」？。

检验解释变量是否存在内生性可以考虑Hausman检验与DWH检验。Hausman检验的原假设为所有的自变量均外生，记OLS为、2SLS中工具变量的估计为，令，用表示的广义逆矩阵，则在原假设成立的条件下应有，其中为内生自变量数量。其中的求法不适用于异方差的情况，异方差时可以考虑用Bootstrap方法求。

DWH检验可以应对异方差情况，所以较之Hausman检验更稳健：所以如果异方差便很少考虑继续使用Hausman检验了。这里便不赘述DWH检验的原理了。

4.5 异方差时的内生性问题与GMM（广义矩估计）

首先，何谓广义矩估计？不严谨地说，GMM是矩估计与WLS的结合体。首先，矩估计的相合性是由大数律保证的，当样本量足够大，样本距与总体矩间的差为一个无穷小量。通过某些阶的矩，可以得到矩估计——这其实是Glivenko定理所保证的，实质上是经验分布函数的功劳（但不保证无偏）。

GMM的想法是自然的，例如，对于正态分布，总体均值就是一阶原点矩、总体方差就是二阶中心矩，自然地想到用样本一阶原点矩与二阶中心矩作为他们的点估计。不过，正态分布有无穷阶矩，而且都是可计算的，那可不可以用更多的矩进行估计呢？当然可以，这就是GMM的思想。譬如同样地估计一元正态分布均值与方差，对一阶矩（考虑均值）有，对二阶矩（考虑方差）有，对三阶矩有，取将其联立为向量函数

易见，用样本矩代替总体矩，得到，再综合考虑各个样本，解方程即可。注意此时这里有三个方程，但只有两个未知数，由于样本总是有限的、不理想的，故不能保证方程组一定有解，于是效仿加权最小二乘法，构造加权损失函数，把使得损失函数最小的参数作为估计，这便是GMM： 其中权重矩阵应是一个正定矩阵，可证明最佳权重应该是。当方程组只取前两个方差、权重矩阵取，得到的正是普通矩估计。

关于GMM更形象、更具象的观点，可参考：如何用简单的例子解释什么是 Generalized Method of Moments (GMM)？。

下面主要讨论在工具变量法中GMM的运用。广义矩估计作为矩估计的推广，可以有效的在异方差与过度识别情况下解决工具变量的问题。如果同方差且恰好识别或过度识别，则GMM等价于2SLS。

为什么在工具变量的估计问题中需要GMM方法？这是因为应用普通矩估计的话，通过矩条件得到的方程在不可识别时有无穷个解，恰好识别时具有唯一解，而当过度识别时无解，因此要解决过度识别的问题，就会考虑GMM——原方程组的限制太强了，导致了无解。通过构造统计量（损失），得到GMM。

GMM需要一些前提条件才能使用，

• 线性假定；
• 记为维的工具变量，由不重复的变量组成，则应渐近独立；
• 工具变量与同期的扰动项相互正交；
• 秩条件：列满秩；
• ，令，则是鞍差分序列（即与过去的所有变量的条件期望为零），且非退化；
• 存在.

4.6 大样本下OLS的性质

大样本下OLS有一些特别的、很好的性质，且条件较为宽松。若满足下述大样本OLS假定：

• 线性假定；
• 维的随机过程为渐进独立的严平稳过程；
• 前定解释变量：, ；
• 秩条件：设计矩阵列满秩；
• ，令，则是鞍差分序列（即与过去的所有变量的条件期望为零），且非退化.

· 注意，最后一个条件中是设计矩阵的一个列向量。

则有

  1). 一致估计（弱相合估计）：估计是依概率收敛的，；

  2). 渐进正态性：；

  3). ；

  4). .

此时即White稳健标准误，

4.7 三种渐进等价的大样本检验：Wald检验、LR检验与LM检验

三种检验都是用以检验约束是否显著的，Engel证明在大样本下三者渐进等价。LR检验的中文译名即大名鼎鼎的似然比检验，LM检验常被译为拉格朗日乘子检验。他们的原假设都是约束成立，备择假设为约束不成立；与此同时，三者的检验统计量的渐进分布都为，其中为维数的个数，或者说约束函数的维数。

说到这里，不得不提提三种检验与F检验的异同，F检验是针对线性约束（最常见的用法是检验系数是否显著为零）且扰动项必须独立同分布于正态分布条件进行的，如果要检验模型是非线性约束的，或者随机扰动不满足正态分布，F检验便失效了，这时应当考虑这一系列大样本检验方法。

三种检验计算的复杂度相差可能是较大的，一般LR检验最繁琐，Wald检验次之，LM检验最易计算。

4.7.1 Wald检验

Wald检验代表着一种区别于似然比检验与Rao得分检验的思路。Wald检验会直接检验约束模型回归系数的MLE与原假设模型（无约束模型）的差异。

当样本独立同分布且，假设有线性约束，则Wald检验的统计量有 其中是对残差（协）方差的估计，可以被看作的二次型，某种意义上，可以讲这样操作目的是标准化。根据的渐进正态性，应当渐进服从，其中是约束的个数。

更一般地，对满足条件的非线性约束，原假设为，首先计算出，接着利用the Delta method（见附录与另一篇文章：重要统计学定理的证明）计算，于是统计量可以被构造： 其中是约束的个数、的维数。

4.7.2 LR检验

似然比检验（likelihood ratio test）通过似然比统计量进行假设检验。与更广泛的、数理统计中的似然比检验一样，其思想是如果原假设成立，显然假设模型与真实模型的似然应该相近，似然比应该接近，则服从分布的接近，若偏离，则应该拒绝原假设。

4.7.3 LM检验

拉格朗日乘子检验（Lagrange multiplier (score) test）通过估计约束模型与辅助回归模型，这让约束后模型形式变得简单的情况下，LM检验更方便计算。在线性回归中，LM检验通常还会建立一个辅助回归模型来计算LM检验统计量的值。

• 首选确定LM辅助回归式的因变量。用OLS法估计问题的约束模型，得到残差，将残差作为LM辅助回归的因变量；

• 其次确定LM辅助回归式的自变量，并建立辅助回归模型。将约束模型中的线性式中残差与因变量对调，即写成的形式，再对回归系数进行最小二乘估计，得到辅助模型的拟合优度；

• 得到LM检验统计量，在原假设成立的情况下，记为约束的个数，有

这部分内容都可以参考高级计量经济学 13：最大似然估计(下)，涉及高级计量经济学，但介绍与证明都较为详细。

4.8 关于计量经济学

计量经济学里，关于线性回归还有很多内容，例如随机效应模型、差分法与混合模型等，限于篇幅，更是限于能力，没法一一剖析。本文关于中级计量经济学的内容只能介绍到这里，即使连冰山一角都算不上，也算记录了一点我的所思所想。

深刻感受到，最“简单”的模型线性回归，根本没那么“简单”！

附录：★★ MSE（均方误差）

设是的估计（不一定无偏），则 容易知道，当是的无偏估计、即时，；

此外，有 于是，MSE综合了方差与偏差（实质上是直接取方差和与偏差平方和的整体和），同时考虑了无偏性与有效性的水平，是一种不错的衡量估计“好坏”的准则。可以认为，MSE是无偏估计有效性的推广，在MSE的准则下可以进行有偏估计与无偏估计“好坏”的比较。

其实MSE被广泛运用还有一定的历史原因，早期统计学发展时由于MSE具有光滑、易计算等良好的性质，因此常常被统计学家用来比较估计，后世沿用了这个方法；但这不能说明MSE准则普遍比其他准则更佳。

附录：渐进理论：the Delta method

the Delta method可以将渐进分布的随机变量转化为随机变量，从而求的样本均值、样本矩函数与协方差等等。

如果且在处连续，则有 用一阶泰勒公式证明。

附录：多元统计分析部分理论的证明

研究统计学，首先一定要具备充分的线性代数能力；作为工具书、课程复习总结，太过基础的内容恕不记叙。

矩阵行列式引理

矩阵行列式引理（Matrix determinant lemma）：设是可逆方阵，、是列向量，则：

Weinstein–Aronszajn恒等式

设是矩阵、是矩阵（与可以是无穷），则： 利用矩阵行列式引理证明。

矩阵求逆引理

设是可逆方阵、是可逆方阵、是方阵、是方阵，则： 结论可以推广到一般的环中。

分块矩阵的逆

设是可逆阵、是矩阵、是矩阵、是矩阵，且是可逆阵，记其逆为，则： 推导是容易的，设的逆为，利用矩阵乘其逆为列出方程，再解出未知元素即可。

当，或，或，或，这个式子有极其简单的形式，而恰好在统计学中这样的情况更多见，比如下文中对多维正态分布的条件分布推导中，我们对协方差阵利用了该式的情形以求其逆；譬如：

  ① 当，有：   ② 当： 此外，即使矩阵、、、的形状与可逆性并非如上所述，逆也是可以计算的。

当是矩阵、是矩阵、是矩阵、是可逆阵，且是可逆阵，记： 当是矩阵、是可逆阵、是矩阵、是矩阵，且是可逆阵，记： 当是矩阵、是矩阵、是可逆阵、是矩阵，且是可逆阵，记：

多元正态分布的条件分布

设服从一个维多元正态分布，有 在此提出一个重要的变换（将在后文解释的构造），变换后能分离解耦两个随机向量：使得变换后与协方差阵为零矩阵而在变换后不变，由此可以导出多元正态分布的条件分布，记： 记，容易验证： 因此与相互独立，于是： 其中；

由上式可解出；记与，注意到： 所以，证毕。

特别地，二元正态分布的条件分布： 换句话说，。

推论：与相互独立；上述一切结论把序号、轮换后仍成立。

题外话：更本质的，提出的思路是想办法类对角化：下做初等变换， 其中，上文中提到到变换矩阵，于是 如此一来，我们便将对角化了：若，则是类对角化的。

抛砖引玉

这篇文章到了尾声，实际上回归的算法千千万万，实在难以一言以蔽之。仅论广义线性回归，还有（针对计数数据的）泊松回归等一众常用线性回归我还没有提到，至于机器学习与非参数回归——那就更多了，比如针对常规数据的k-近邻回归、随机森林回归、LOWESS稳健回归与局部多项式回归，针对生存分析的AFT算法、Cox模型，乃至Booting系列算法、神经网络算法与深度学习算法。限于能力与精力，没办法在这篇文章中涉猎更多内容，如果以后有机会，再写一些吧！不过，应该是没有这份机会了。看起来，毕业后我所从事的行业，可能令我不会再用到这些知识。

另一参考

单击此处跳转：《总结归纳：回归分析》

注：上面这篇文章的可参考性就不大了。

本文最初是在这篇文章的基础上修订与增补而成的，但在写这篇文章时作者才刚刚接触线性回归不久，可以说这篇文章其实只是作者的学习笔记，有些理解是明显错误的