支持向量机的一些并不算深入的基本数理理论，包含SVM、SVR与LS-SVR。支持向量机具有非常强的数学与统计理论支撑，研究SVM的数理理论对加深对SVM的理解是大有裨益的。

在我们开始以前，我想谈谈关于我与统计学。作为西南大学数学与统计学院统计系的学生，在修完数学课程如实变函数论、近世代数与泛函分析后，学院相继为全体学生开设了最优化理论、统计计算、多元统计分析与回归分析等多门统计课程，唯独不统一在学院开设机器学习。优化理论与统计计算算法在机器学习中扮演了重要角色，譬如大名鼎鼎的拟牛顿法之代表BFGS算法、用于非凸优化问题的退火算法和遗传算法都有广泛的应用，但修习了这些理论却不开设后续课程实属遗憾，这些理论当然也就没有了用武之地，成了一纸空谈。通过参考多方资料，我在没有教师帮助下独立探索了一些机器学习理论，希望结合数学理论与数理统计学方法，加深对机器学习的理解。本文主题是记录一些我关于“SVM”的想法与感悟，由于才疏学浅，只能做到泛泛而谈，如有纰漏与谬误恳请与我联系。

个人认为，许多机器学习算法都或隐或明地蕴含了不少的数学与统计思想，如SVM的优化涉及最优化理论与统计计算算法（退火算法、遗传算法），核函数的提出源自Hilbert空间算子理论，正则化与空间息息相关，核方法的理论支持Mercer定理更是一个经典的泛函分析定理。本文大概读者具有一定的回归分析基础、优化理论基础与泛函分析基础时，阅读是没有问题的。

鹦鹉学舌也好，拾人牙慧也罢，普通学生，普通家庭，确实没有动力与能力独立开创、推广新的理论，这篇文档的意义可能是十年后再回首，说明本科时的我曾经有试图学习些什么过吧。

为方便表述，记表示的范数的算术平方根，即欧氏空间意义下的距离；

MSE：均方误差，，当估计无偏时，有，即方差之和。MSE综合考虑了无偏性与有效性，是常用的评估标准；

维空间的超平面：维子空间；

广义拉格朗日乘子法与KKT条件：用隐函数组定理是容易证明的，在任意一本数学分析与最优化理论教材都有证明过程；

如无特殊说明，本文用表示样本量大小。

1. SVM（SVC）

1.1. SVM概论

1.1.1. SVM的思想

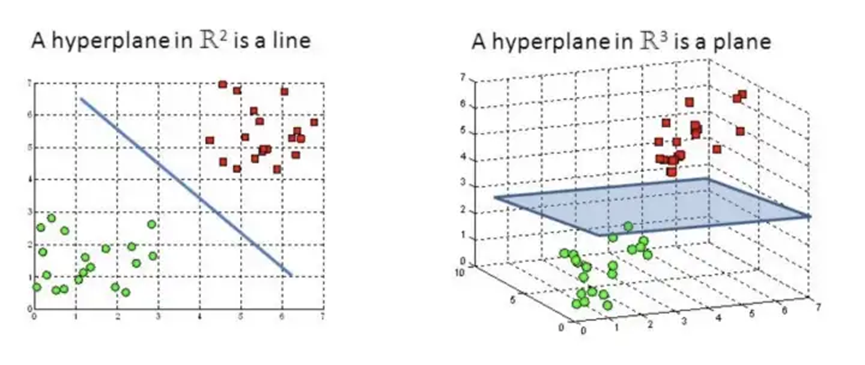
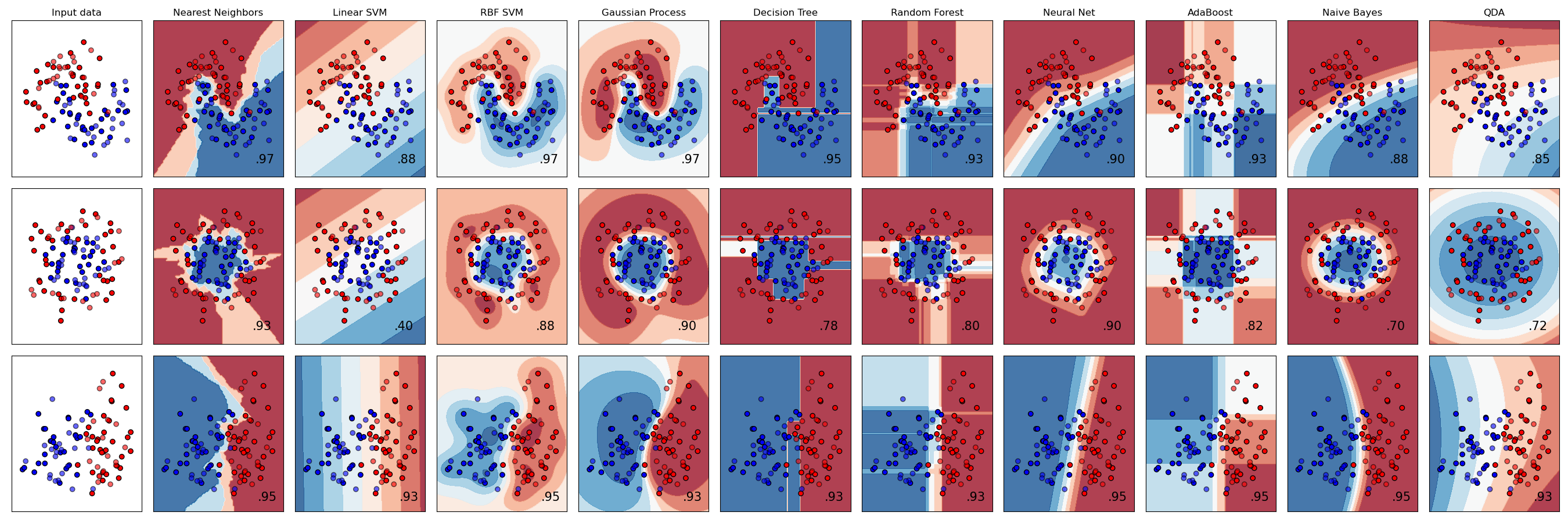
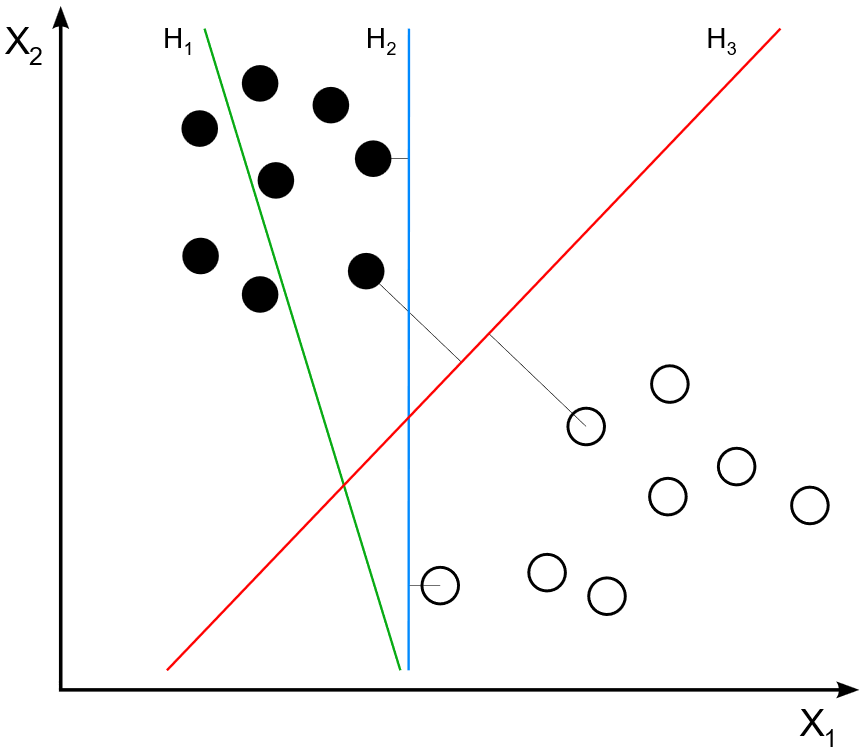
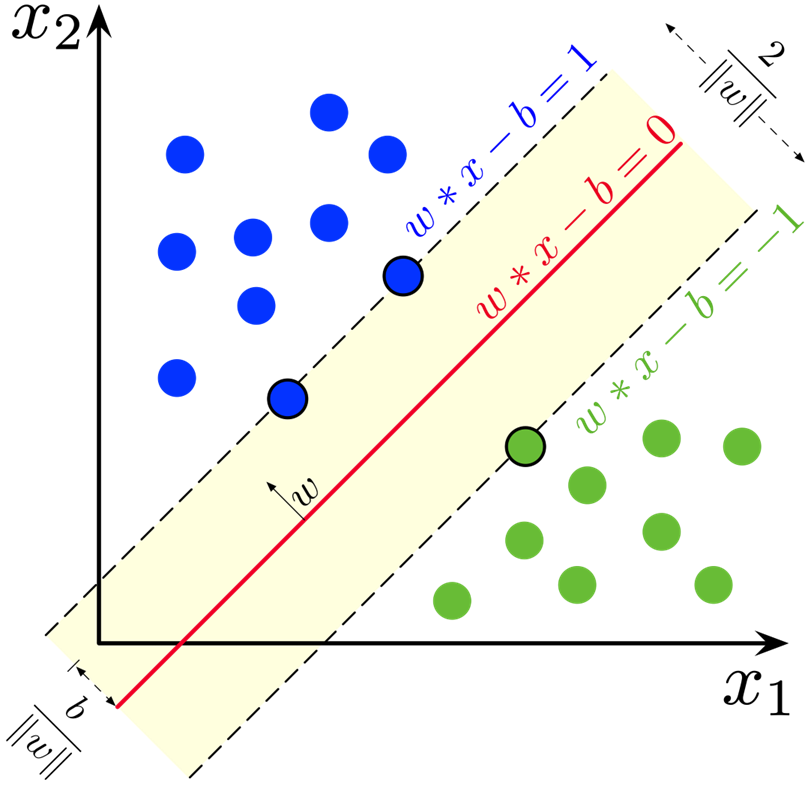
SVM（支持向量机，Support Vector Machine）是一种有监督学习方法，属广义线性分类器家族，其目的是对数据进行二分类，既可以通过寻找一个当前样本空间的分割超平面进行线性分类，也可以通过核方法在更高维空间中寻求高维超平面进行非线性分类，并且可以被应用在回归分析。在我看来，SVM的想法是自然的，这与线性回归中OLS的思路如出一辙。如果说OLS的目的是获得使得RSS最小的估计，则二分类SVM的目的是获得某个超平面，使得其两边支持向量到超平面距离最大且相等。在高斯-马尔可定理条件成立情况设下，线性模型的OLS得到BLUE，误差在MSE意义下最小，对于良好的数据集大部分样本点都应该以较小的距离分布在拟合直线两侧；而SVM试图找出一个高维的超平面，使两类样本距离这个超平面最近的距离相等且最大，如下图所示。显然，三条一维直线中的划分要优于和，拥有更强的分类能力。

但OLS与SVM并非高度一致，在信息利用上有明显的差异：OLS的预测利用了所有的样本（最小化RSS），而SVM只利用到了支持向量，非支持向量的任何改变都不会对结果产生丝毫影响。

1.1.2. SVM在应用中的的优缺点

SVM在小样本、非线性以及高维模式识别等方面有出色的表现，且容易结合其他方法进行推广应用，在文本、超文本分类与生物、医学及其他科学领域已经有了广泛的运用，一些浅层语义分析也基于SVM，样本量适中而特征数不算多时有很好的分类能力；

SVM的潜在问题包含，作为彻底的有监督学习、能利用的样本必需有完整的标记（决策树方法不需要），只适用于二分类任务，得到的模型参数难以得到现实意义的解释（业务上线性回归参数便有极强的可解释性，SVM通常不能做到），对缺失数据敏感。

同时，SVM的优化目标为一个二次凸优化，有良好的凸优化性质（优化算法一定收敛到唯一全局最优解），但这也使得超大样本量情况下SVM求解异常困难，使带有核方法的SVM理论实践复杂度不低于；SVM通过核技巧一定程度避免了维度诅咒，但核技巧不是SVM的专属；对于扁平化数据，选择适合的核函数与正则化方式至关重要，否则非常容易导致过拟合，这是SVM最大的变数。

与一些神经网络算法不同，SVM目前已有严格的数学与统计理论支持。SVM基于Vapnik 和 Chervonenkis提出的Vapnik-Chervonenkis 理论（下称VC理论）与结构风险最小原理，属于非概率二元线性分类器，并没有严格按照随机抽样的原则抽取样本，无法确定抽样误差，因此大数律与中心极限定理等极限理论也并不适用；同时这令他并没有过分在意样本空间的维数，以至于为了达到非线性分类的目的可以多次升维，而且折中了精度（Accuracy）与学习能力的原理令SVM有较好的泛化能力，但这需要对SVM进行一些改进以达到更好的效果，比如软间隔的方法。

此外，由于非线性核的SVM理论上时间复杂度不低于，所以对极大的样本量非线性可分情况SVM的训练是困难的（虽然只利用了支持向量，但在确认全部可能的支持向量以前我们并不直到哪些向量是支持向量），因此人们基于SVM理论研究出了多种近似算法，比如CVM、随即傅里叶特征算法、Nyström算法等。

1.2. 支持向量

假设我们需要找到的分割超平面为，其中为超平面的法向量（不一定单位化）；从空间解析几何角度看，表示超平面的方向，表示位移，即超平面到远点的距离。

根据空间解析几何理论，样本空间中任意一点到超平面的欧式距离为不妨设因变量取值为或，如果超平面能正确对样本进行分类，方便起见，我们希望找到一个超平面，使得当则样本点位于超平面“下方”，；当则样本点位于超平面“上方”，，即 $此时此时$ 可以将两个不等式综合为一式，方便我们后续解决优化问题（这里也能看出，为什么我们设的值域为）；此外，易见在这样的定义下，恒有。

令使得式中任意一不等式等号成立的样本为支持向量（Support Vector），直观上看支持向量全部落在决策边界上，是距离超平面最近的一组样本。当确定，仅与有关，由距离公式与所定义的式得出，支持向量一定满足（当且仅当时距离最小），因此两个互类支持向量到超平面距离之和为，称之为间隔，可以认为间隔是互异决策边界的距离。 $间隔$

1.3. 优化问题

SVM中一般考虑对直观下约束优化问题的拉格朗日对偶问题优化，相对原优化目标效率更高，这里有一点需要解释，关于为什么我们考虑对偶问题：我们可以不从原问题的对偶问题出发考虑求解，例如线性核SVM的原始优化问题为下文的式，从标准的不等式约束二次规划（QP问题，QP模型）模型来看令二次规划当下是非常成熟的理论，对于线性核SVM，线性等式约束下的原优化问题可以通过矩阵直接求解线性方程组，对于线性不等式约束也有内点法、增广拉格朗日函数与梯度投影法等多种方法可用以配合求解，这样可以在不利用对偶问题前提下得到解；。但在引入非线性核函数后，一是可能映射到高维空间后不能保证的正定性，而维数如果足够高时这个问题变成了NP难题，局部最小点也不一定唯一；与此同时，如果我们希望考虑广义的拉格朗日乘子法求解，记广义拉格朗日函数为，这相当于把不等式约束并入了优化目标式中，这时解原优化问题等价于解这个式子中的作用只是限制原本约束式对优化的影响，对偏导以试图解出不难看出，我们只得到了一个支持向量，满足，因此原问题的拉格朗日函数优化较为困难；如果我们考虑他的对偶问题，这等价于求解不过，对偶问题的最优解可能不是原问题最优解，根据优化理论我们有，万幸的是原问题本身就是一个二次规划问题，属于强对偶，所以等号严格成立。关于优化问题将在后文再细致讨论。

大体上，我们的求解办法是通过优化方法计算出对偶问题的解（即），然后代入KKT条件计算出，再同时将拉格朗日乘子与解得的代入KKT条件的稳定性条件即解出，至此我们得到超平面的解析式。

1.3.1. 支持向量与对偶问题

容易想到，一般分割超平面间隔越大，分类能力越强，因为越大的分割对误差有更大的容许，对噪声导致的数据波动有更高的忍耐，而不至于某样本稍稍偏离主体便被错误划分为另一类。

直观来看，为了找到这个最合适的超平面，我们需要解决一个如下的约束下最大化分隔的优化问题值得注意的是对这个优化问题的结果也有影响，考虑到，因此的大小确会影响约束优化的解。为了方便优化，我们希望将其转化为一个凸优化问题，考虑到最小化与最大化是等价的，于是可以改写求解超平面问题为由凸优化理论，拉格朗日对偶函数一定是凹函数、弱对偶的，且凹性与原目标函数与约束无关；当原优化问题为凸优化问题时，即满足Slater条件，拉格朗日对偶问题一定是强对偶的，便是一个典型的凸优化问题，因此其拉格朗日对偶问题与自身等价。再考虑到SVM优化目标，考虑他的拉格朗日乘子的优化比直接考虑的优化更简便，对偶问题处理起来也会更高效（也能看出拉格朗日乘子具有一定的约束意义，能帮助我们讨论模型），下求解的拉格朗日对偶问题，这根据最优化理论不难求出，应用广义拉格朗日乘子法，首先写出不等式约束问题下的拉格朗日函数分别令对与偏导为，得到、 $稳定性条件$

$稳定性条件$

$原问题可行性对偶问题可行性互相松弛条件$

、、联立即的KKT条件（可认为是全局最优解的约束，从而间接得到的最优解），最终由、得到的拉格朗日对偶问题需要注意的是，KKT条件是原问题最优解的必要条件，当原问题是凸优化问题时当然是全局最优解（此时局部最优解与全局最优解等价），对于强对偶问题的拉格朗日对偶问题的最优解也一定满足KKT条件，这是为什么在这里可以认为拉格朗日对偶问题加上KKT条件的约束便得到全局最优解的原因。

注意到，的限制使得如果某点的拉格朗日乘子，则必有，即此样本点为支持向量；若有则一定有，进一步观察Wolfe对偶问题可以发现拉格朗日乘子为的样本点对优化问题没有任何影响只有拉格朗日乘子非的样本点对于优化问题有意义，这表明了SVM的一个极其重要的性质：只有支持向量才会影响超平面的选取，而不在分割边界上的任何一点对超平面的选取都不产生任何影响，这也是SVM——支持向量机名字的由来。

容易看出也是一个二次凸优化问题（实质上这是优化理论所保证的），实际应用中一般考虑二次规划优化算法求解，比较高效的算法有次梯度下降法、坐标下降法和SMO算法等等，其中，今天SMO算法对于SVM问题较为流行，他的思想与坐标下降法有异曲同工之处，关于优化算法在附录再稍做介绍。

值得一提的是，SVM之所以在高位模式识别领域具有优势，是因为面对维数诅咒SVM只利用了比较少的样本（只利用了支持向量）。通常对于高维数据，常用的方法有① 特征选择，如Lasso回归；② 直接降维，如PCA、MDS、LLE；③ 正则化，以减轻高维样本空间带来的多重共线性等不良影响；④ 增加样本量，深度学习便是沿着这个思路；在今天大数据的时代下，一个大型深度学习模型拥有上百亿个参数都不足为奇。

1.3.2. 参数与的解及预测

求参数的解我们仅用到了支持向量，因此在优化求拉格朗日乘子完成以后，我们需要的样本便只剩下支持向量了。

对于，在通过求解优化问题解得后由直接得到，理论上只需要考虑为支持向量的样本（否则其拉格朗日乘子为，与和式结果无关）；

对于，我们知道对任何支持向量，都有，结合，有为了利用更多的样本以增强稳健性，常常使用全部的支持向量计算以减轻误差、噪声等因素带来的影响；记支持向量的集合为，势为，则有上式可认为是利用所有支持向量分别求解后取他们的算数平均值。

在通过算法求出、与后，由式即可得出我们所需要超平面的解析式：记所求超平面为，则

这一章节中所有需要预测的样本，都代入式的便能得到结果；如果存在多种拉格朗日乘子、、，这是后文软间隔与SVR中的情况，则将形式上代入式中即可；如果涉及到核方法，则

注意代表训练集的第个数据，即的第行（而不是第个分量），这时一个新数据的预测分类为 $此时此时$

1.4. 核方法

1.4.1. 核方法的思想

目前为止，我们的SVM算法只能求解线性分类问题，比如“且”问题、“并”问题与“非”问题，但“异或”这样的非线性分类问题并没有办法解决，从我们的思路与式可以观察出现在我们只是在当前样本空间中寻找合适的分割超平面，譬如有两个自变量与的分类问题里，从出发我们只能得到平面图的一条直线的分割，而当样本类别分布的分界线呈现出明显的O形，我们目前的方法便不再可行了。

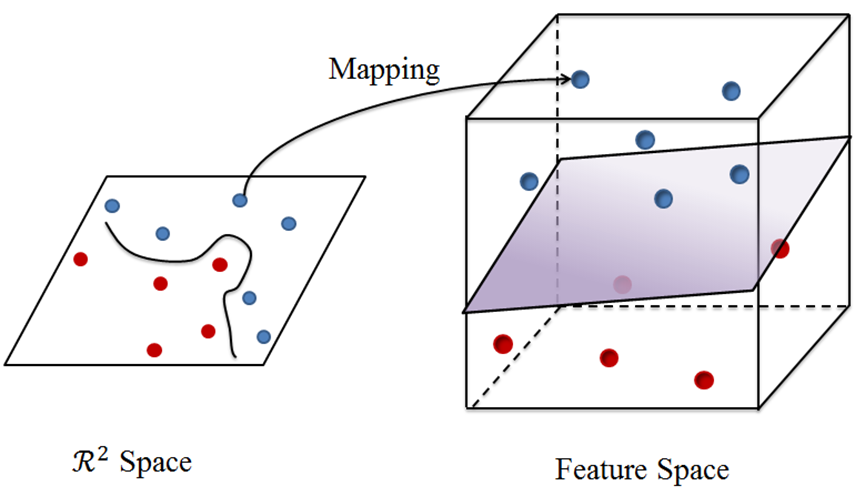
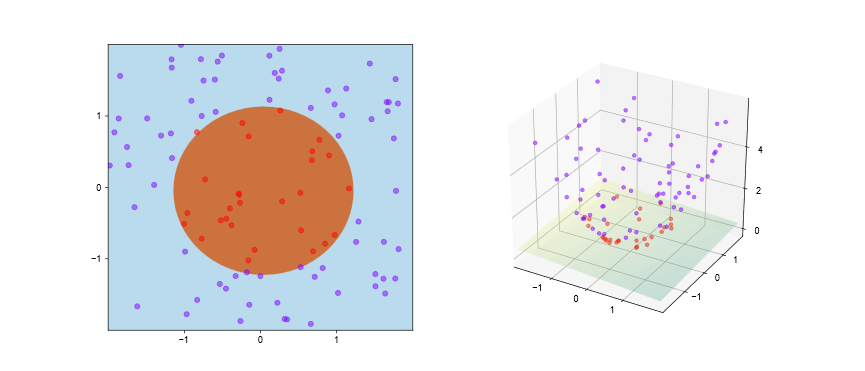
不过我们仍有解决办法让SVM有能力处理非线性分类问题：我们可以将样本空间映射到一个更高维的空间，使样本在这个更高维的空间可分，例如下图左部分的分类问题，当我们把二维的自变量空间升至维，即下图右部分，便能够找到一个超平面使得样本可分；如果升维仍不线性可分，可以继续升高维数。升维时是可以将样本映射到无穷维空间的。

对于有限维的样本空间，即属性数或者将向量的分量数是有限的，则必存在一个高维空间使得样本线性可分，这是显而易见的，只不过可能在这一高维空间下的内积难以计算。

对于非线性分类问题，用表示将映射至高维空间后的特征向量，需要寻得的高维空间下新超平面为，于是得到高维空间下的优化问题、，把、的替换为即可。中涉及到高维空间下的内积计算，这可能不是很好解决，因为SVM在升维的时候可以升至极高的维数甚至无穷维，用计算机计算无穷维的向量内积并不现实。不过不要担心，我们可以通过核技巧（凡是涉及升维内积计算都可以运用核技巧，如分布式运算、深度学习中的运用）绕过这个障碍。我们可以试图找到一个函数称之为核函数，使得从而避开对升维后内积的直接计算，如果能够找到这样一个核函数，那么优化问题进一步转化为。则由用替换中后的式并用替换推导，或直接对式做同样替换，得到我们称之为支持向量展式看上去，只要我们能找出这样一个合适的核函数，就能由式，通过训练样本中的核函数展开得到最优解，故而我们仅需要针对支持向量这少量的样本寻找一个合适的核函数，而不需要关心具体是何种映射。接下来的问题是，我们是否总能找到这样一个核函数？或者，我们如何找到这样一个核函数？

核函数的Mercer定理：二元对称实值函数是核函数当且仅当对任意一组向量的核矩阵半正定。

Mercer定理确保了这样一个核函数必定存在，但是否可行、如何寻找最佳核函数，同岭估计最佳岭值的确定一样目前没有普遍适用且最佳的方法，这是值得研究的问题。现在有一些综合多种常用核函数考量的技术，这借助了集成学习的算法。

1.4.2. 核方法的泛函分析理论支持

这一部分是纯粹理论的推导，如果不关心底层理论可以略过，毕竟这需要一定的数学基础；

希望这部分读者拥有数学及相关专业本科生或理工研究生以上的泛函分析水平，起码对泛函延拓定理要有所耳闻。

1.4.2.1. 核函数与Mercer定理

Mercer定理确保了只要一个对称函数对应的核矩阵半正定，那么他就能被当作核函数应用，这是核技巧的关键，是核技巧得以存在的理论支持。事实上，定义核函数等价于定义了一个RHKS（再生核的Hilbert空间）。

首先定义核函数，若二元实值可积函数满足正定性与对称性，则称为空间上的一个核函数。记某组数据关于一核函数的核矩阵为由核函数的定义知道，一定是半正定的矩阵。

现在让我们把核矩阵定义推广至任意一个二元实值对称函数，如果他的核矩阵对任意一组数据保持半正定，则由定义他便是一个核函数，所以对于二元对称实值函数而言，其为核函数与其核矩阵总半正定等价，这便是Mercer定理的特例，也是我们需要的结果。

离散形式的二元Mercer定理：设是上的二元实值对称半正定核函数，即，满足① ，② ，假设在上连续，不妨设，则存在的一族连续标准正交基及单调递减趋于的的非负列使得，，并且这个级数在上一致收敛，为Lebesgue测度。

离散形式的二元Mercer定理很容易推广到更一般的测度空间上，事实上Mercer定理是Hilbert-Schmidt定理的特殊情况，鉴于本文并不是泛函分析教程，不再赘述；证明Mercer定理可以考虑Mercer定理的条件满足Hilbert-Schmidt定理的条件，这需要几个引理与共鸣定理。

Mercer定理参考：https://johnthickstun.com/docs/mercer.pdf

[John Thickstun, MERCER’S THEOREM]

Hilbert-Schmidt定理参考：https://core.ac.uk/download/pdf/82400668.pdf

[José L. Martínez-Morales, The Kernel Theorem of Hilbert–Schmidt operators, 2003]

1.4.2.2. RKHS（再生核Hilbert空间）

我们知道次Lebesgue可积函数可以视作无穷维向量，譬如设，由于具有可数个完全规范正交系，如正交三角函数系，，，，，，，故有（广义）Fourier级数因此次Lebesgue可积函数作为无穷维Hilbert空间的一个元素，故可以被视为无穷维向量同样地，推广到二元核函数上，不妨设：，可以被视为无穷维对称矩阵，记做，由于的正定性，这个无穷维矩阵也是正定的，故可进行特征值分解并且有可数个特征值，记为，，其中是对应特征向量列成的矩阵，容易知道是的正交基，因此有，这样也能导出Mercer定理，当然这里推导并不严谨，仅作启发思路。

当我们把作为一组正交基，称为RKHS（再生核Hilbert空间），由此可见任何核函数都应该在RKHS中，而名称中的“再生”体现在

1.4.3. 常见的核函数

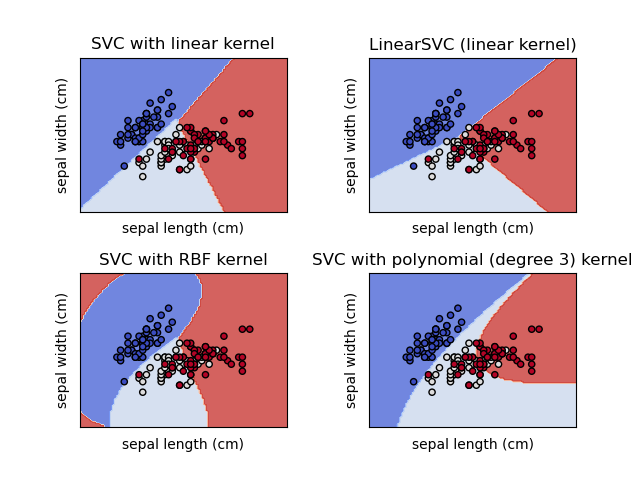
理论上，如果知道了映射的选取，便能确定一个最佳核函数；但许多时候这并不容易做到，下列部分常用的核函数，在一些特定情况下能取得不错的效果。除线性核外，统称非线性核。

一些常见的核函数	函数形式	注解
线性核		即多项式核在时的特例
齐次多项式核
非齐次多项式核
径向基函数核，RBF核（高斯核）		为了参数化，可以令，注意RBF核与正态分布没有任何直接关系
拉普拉斯核
双曲正切Sigmoid核

除了上述核函数，还有字符串核函数、核函数、直方图交集核函数等多种核函数可以考虑。

核函数的一些运算性质，使得我们可以通过已有核函数构造获得更多新的核函数：

① 若与是核函数，则，仍是一个核函数；

② 若与是核函数，则仍是一个核函数；

③ 若是核函数，则，仍是一个核函数。

既然核方法如此强大，为何我们不在逻辑斯蒂回归中也大量运用？这是因为SVM优化问题的拉格朗日对偶问题便于使用核方法，而逻辑斯蒂回归的损失函数交叉熵核化后难以优化求解，甚至不能确定凹凸性。

经验上看，用代表样本量、用代表特征数，我们有一些规律：

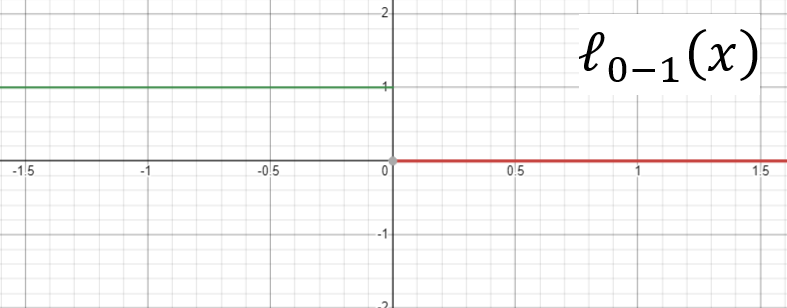
(1) 如果较之小得多，此时训练集不足以支持SVM得到一个较复杂的非线性模型，这时考虑逻辑斯蒂回归、线性核SVM；

(2) 如果不算小但也不充分大，而较小，譬如取而取，则RBF核表现往往不错；

(3) 如果较大而较小，例如大于而介于与之间，这时SVM二次规划的计算量大，优化速度劣势明显，解决措施可以考虑增加特征的数量，再应用逻辑斯蒂回归或线性核SVM；

(4) 逻辑斯蒂回归与线性核SVM算法相似，但在样本量高达数十万时线性核SVM表现通常比逻辑斯蒂回归好。

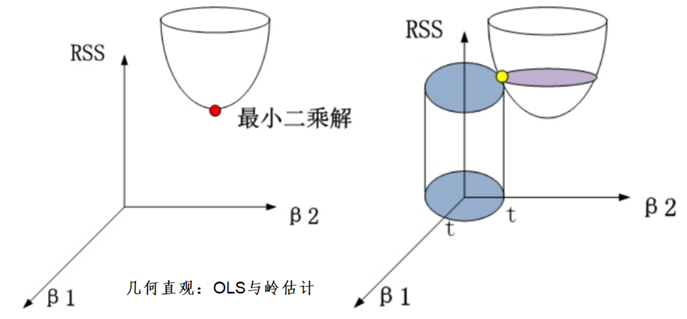
1.5. 软间隔与正则化

软间隔与正则化都是对付过拟合的手段。

1.5.1. 软间隔

上文提到了一个问题：虽然我们可以通过核方法将样本映射至高维使得样本在高维空间线性可分，但我们还不能确定该选用何种核函数较为合适，也不能确定究竟要将样本映射到多高维的空间能使得其线性可分。同时，目前我们的SVM方法过于严格，因为我们要求分割超平面必须考虑所有的样本点来寻找支持向量。这可能在实际情况下并不太实用，因为非常容易造成过拟合的问题，让SVM学习到一些本不应该学习的、仅出现在特定样本的特点。

通过允许一些SMV在部分样本上“犯错”，即让部分样本突破限制而使得其满足，这种方法称之为软间隔；相应的，前文中严格要求，必须满足，即所有样本都必须严格“正确”划分而不能“犯错”，这种方法称之为硬间隔；同时，我们需要保证不满足约束的样本应该尽量少一些，否则会产生极大的偏差。

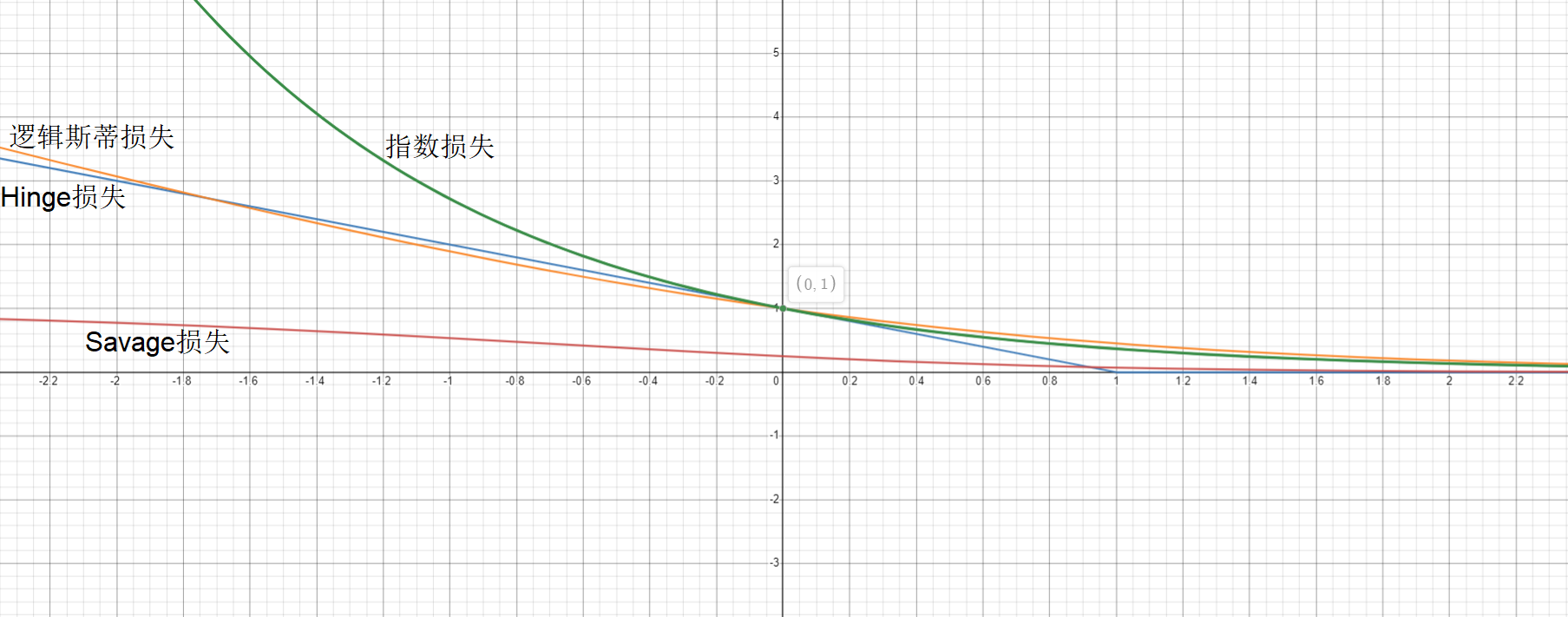
1.5.1.1. 替代损失

为了达到上述目的，我们对的限制做进一步处理，得到软间隔的原始优化问题：其中是我们最大能容忍的满足的样本点个数，即最大的允许SVM犯错次数；则为一个控制，不等式左边的和式为一个计数器，这个计数器仅对满足的计数，即SVM犯错的次数。显然最自然、最直观的是损失函数。

但这个函数解析性质较差，不方便推导，也不易优化求解，常用其他函数替代，称为替代损失，为了有良好的优化性质，一般都期望替代损失是凸函数；SVM需要的替代损失还要求在取值为正时应以较快的速度收敛至

一些的替代损失	函数形式	注解
Hinge损失（铰链损失）		Hinge损失的应用非常常见，但得到的解较为稀疏；有时取其平方
指数损失
逻辑斯蒂损失（lnistic损失，对数几率损失）		对异常值不敏感
Savage损失

上述替代损失除Savage损失已于2004年被证明与经验风险最小化问题是一致的，即通过求解替代损失函数仍是原问题（损失函数）的解。

由于Hinge损失在以后值严格为，因此Hinge损失倾向于得到稀疏的解，得到非零分量尽可能少的解；如果使用逻辑斯蒂损失，则SVM结果与逻辑斯蒂回归非常相似，可以发现他们的优化目标是大同小异的，但与逻辑斯蒂回归不同的是SVM的参数通常没有那么强的实际意义。关于逻辑斯蒂回归如果在今后有时间，我会把我已经写好的文档重新用Markdown整理一遍，这是关于属性数据分析的文档，文中着重推导了逻辑斯蒂回归。

对应用拉格朗日乘子法，得到等价的优化问题这里的意义与式中的意义是相似的，他们都可以视为拉格朗日乘子，越小，约束对优化的结果影响越小（因此也可以被理解为约束对结果影响的权重），容许SVM犯错的机会越大，结果越倾向于犯更多的错误，与硬边距结果相差越大；越大，约束对优化的结果影响越大，对SVM正确率要求越严格，结果越倾向于犯更少的错，结果越与硬边距q看相似。

可以认为 $式式$ ，即当取正无穷大时等价于不允许SVM犯错，即硬边距情况，当取充分大的有限值时SVM的行为类似硬边距情况，但仍会学习分类的规则是否可行。值得一提的是，这一步的操作与岭回归中由约束下最小二乘估计导出岭估计的损失函数的操作是相同的。

一般来说，取较小值时SVM会忽略更多的“异常”样本，或许会得到一个更“好”的决策边界。

从结果上看，较大会使较小，可能导致过拟合、高方差；较小会使较大，可能导致欠拟合、高偏差。

1.5.1.2. 松弛变量与软间隔SVM

这里考虑应用Hinge损失，引入松弛变量（即），于是可以改写，得到软间隔SVM的优化问题式成立时，若样本的松弛变量不为，说明SVM允许了一次“犯错”，且松弛变量越大说明“犯错”的程度越重，允许“犯错”的最大程度与有关。类似的，为了看出与硬间隔的联系，可以导出的拉格朗日对偶问题的最优解一定满足KKT条件，与上文同样的操作，可以得知这个问题的KKT条件为

$稳定性条件稳定性条件稳定性条件原问题可行性对偶问题可行性互相松弛条件$ 观察与，可以发现在硬间隔与软间隔问题之间，他们的不同仅在于对拉格朗日乘子的约束不同，软间隔方法较之硬间隔除了限定，还要求，这是的另一个意义——限定所有样本对应的拉格朗日乘子的最大值。

软间隔具有非常广泛的应用，能有效降低过拟合带来的影响，使得SVM不会学习太多特定样本的特征。实际应用中大多数两类样本的分布很可能是糅合的，如果不允许SVM在特定样本上稍稍“犯错”会使得把这一特定样本的误差、噪声、极端分布等因素通通不加筛选地学习，这大大降低了模型泛化的能力。

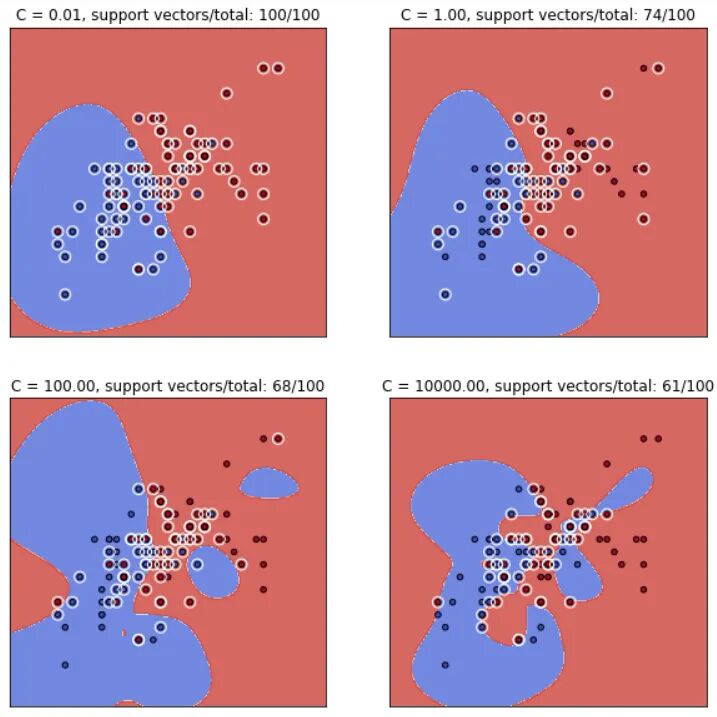
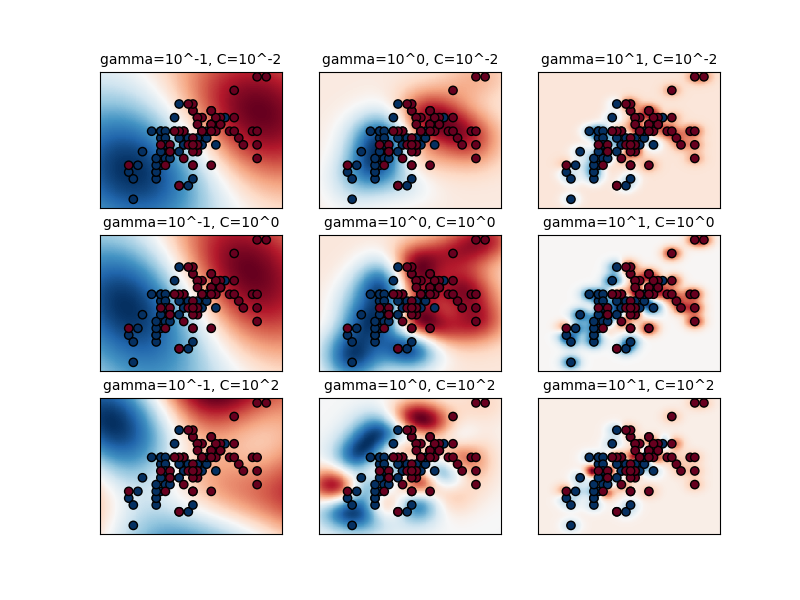
径向基函数的支持向量机分类效果关于的变化如下：

可以看出，随着的增大，判定边界变得愈加复杂，过拟合风险越大，支持向量数量相对减少：越大，SVM对误差的惩罚越重、容忍度越低，这时SVM越“严格。当，带软间隔的SVM等价于不带软间隔的SVM，这时对误差“零容忍”。

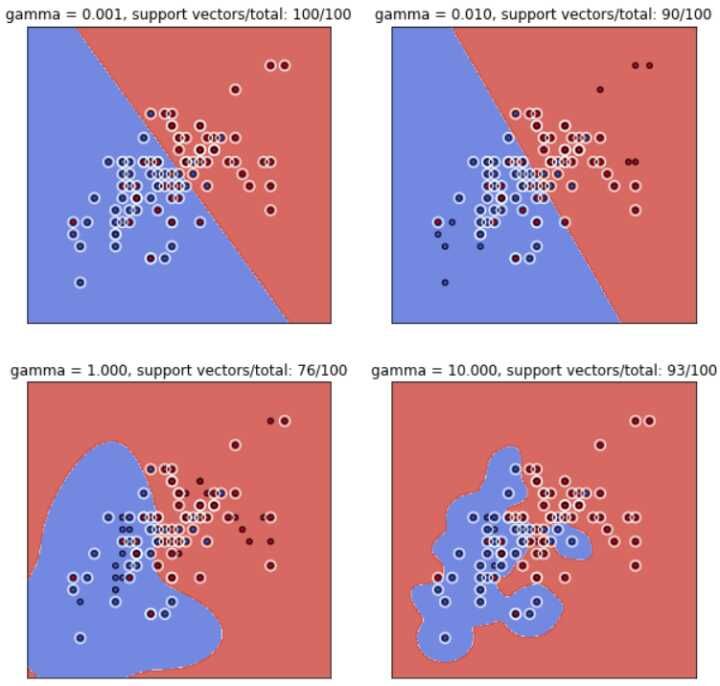
径向基函数的支持向量机分类效果关于的变化如下：

可以看出，随着的增大，判定边界变得愈加复杂，过拟合风险越大，支持向量数量先减少后增加：代表每个支持向量的影响范围倒数，很小的时候，每个支持向量影响范围极大，这时决策边界近乎线性，进而可能存在欠拟合的问题；当较大，每个支持向量影响范围很小，这时支持向量便非常之多——换言之，“人人都是支持向量”，这也会带来严重的过拟合问题。

综上所述，可以得出一个推论：单单凭借支持向量的个数是不能判断RBF核SVM是否过拟合或欠拟合的。

直观体现如下，阴影代表支持向量影响范围：

1.5.2. 更为一般的正则化的观点

首先我们提出更一般的优化目标称结构风险，与模型本身性质有关；称经验风险，描述模型与训练集数据的联系，控制其较之结构风险对结果影响的的权重。

结构风险蕴含了我们希望模型具有何种属性的目的，例如在SVM中结构风险通常取根号下的范数，即正则化，因此前文的所有公式实际上都暗暗包含了正则化的过程，这将倾向于得到非零个数相对稠密的解；我们也可以取其余的范数甚至其他的方法进行正则化，例如、范数，这又倾向于得到相对稀疏的解，即非零分量数尽可能少。范数的定义源自实变函数论与泛函分析，不同的正则化有不同的最适场景，没有绝对的优劣之分，这在线性回归中也有体现，一般提到的线性回归我们都采用OLS的办法估计模型的参数，即最小化RSS——残差的范数，但没有任何证据表明整体上最小一乘法一定便劣于OLS，只不过OLS数学性质较好，易于推导，并且在高斯-马尔可夫定理的条件成立情况下有非常良好的统计性质；在OLS基础上进行正则化得到岭估计，即取，在OLS基础上进行正则化得到Lasso估计。

经验风险有助于削减假设空间、降低过拟合风险。

式便是大名鼎鼎的正则化问题的数学定义，称为正则化项，称为正则化常数，从罚函数的观点来看，其实是给予了两种目的不同的惩罚；正则化也可以认为是模型的先验概率。

VC理论介绍：https://www.cs.cmu.edu/~epxing/Class/10701/slides/lecture16-VC.pdf

关于VC理论更多的信息可以Google “Vladimir Vapnik”.

VC理论经典文献参考：http://www.mit.edu/~6.454/www_spring_2001/emin/slt.pdf

[Vladimir N. Vapnik, An Overview of Statistical Learning Theory, 1998, IEEE]

1.6. SVM多分类问题

SVM作为二分类分类器被提出，要进行多分类可以考虑一对一One Versus One利用得分或DAF（有向无环图）输出结果、一对多One Versus the Rest组合出结果；现在也有一些“直接”多分类的SVM变种方法，目前这些方法需要的算力很大，花费的时间仅在小样本下可接受。

Multiclass SVM aims to assign labels to instances by using support vector machines, where the labels are drawn from a finite set of several elements.

The dominant approach for doing so is to reduce the single multiclass problem into multiple binary classification problems. Common methods for such reduction include:

Building binary classifiers that distinguish between one of the labels and the rest (one-versus-all) or between every pair of classes (one-versus-one). Classification of new instances for the one-versus-all case is done by a winner-takes-all strategy, in which the classifier with the highest-output function assigns the class (it is important that the output functions be calibrated to produce comparable scores). For the one-versus-one approach, classification is done by a max-wins voting strategy, in which every classifier assigns the instance to one of the two classes, then the vote for the assigned class is increased by one vote, and finally the class with the most votes determines the instance classification.
Directed acyclic graph SVM (DAGSVM)
Error-correcting output codes

Crammer and Singer proposed a multiclass SVM method which casts the multiclass classification problem into a single optimization problem, rather than decomposing it into multiple binary classification problems. See also Lee, Lin and Wahba and Van den Burg and Groenen.

2. SVR

2.1. SVR概论

2.1.1. SVR的思想

此前我们讨论的SVM是从二分类问题出发的，即所谓的SVC，Support Vector Classification，支持向量分类。这里我们着重探讨SVR，Support Vector Regression，即支持向量回归，是将SVM技术应用在回归分析的一种方法，是一种有监督学习。

1996年，Vladimir N. Vapnik、Harris Drucker、Christopher JC Burges、Linda Kaufman 和 Alexander J. Smola提出了将SVM应用于回归的方法。

种种经典的（广义）线性回归模型，包括岭回归、Lasso回归、Elastic Net回归与逻辑斯蒂回归等等，都有一个共同的特点：当且仅当预测值与真实值完全相同时，损失才为，否则有越大的偏移，会产生越大的损失；而在SVR中我们允许预测值与真实值存在可容忍的最大偏差，只有当真实值越过以预测值为中心上下至多偏差时损失才开始增大，而若则损失为零，此时我们认为预测值是正确的，在一个可容忍的范围内。换句话讲，所有的与形成了隔带，只对真实值在隔带以外的样本点计算损失。

在SVR中，最佳拟合超平面就是容许至多偏差范围内，具有点数最多的超平面。

2.1.2. SVR在应用中的优缺点

通过控制可以人为控制容忍偏差，在容忍偏差范围内对误差不敏感，是一种比较“宽容”的回归模型；同SVM一样，利用核方法巧妙避开了维数诅咒；同时，SVR也对参数与核函数选取较为敏感，人为选取的参数与核函数是否合理可能使得结果大相径庭，二次规划的优化目标使得SVR的解也有良好的凸性，但也导致大样本下计算困难。

而且SVR对数据缺失较为敏感，不能很好的利用邻近数据对缺失数据的趋势进行良好的拟合。

2.2. 优化问题

2.2.1. 对偶问题

对于SVR，根据前文的分析，我们从软间隔SVM的优化目式出发，通过令“用来计数的替代损失”具象化为“”达到仅针对使得的样本点计数，称为-不敏感损失函数我们提出SVR的原始优化问题类似地，引入松弛变量，考虑到隔带两侧松弛程度可能不尽相同，我们用两个松弛变量与分别控制隔带两侧的松弛程度，改写，为方便表示这里用表示经过SVR得到的预测值（估计值）与上文相同，令的拉格朗日函数分别对、、与偏导为，进而导出的拉格朗日对偶问题的最优解一定满足问题的KKT条件 $稳定性条件原问题可行性对偶问题可行性互相松弛条件$

2.2.2. 参数与的解及预测

同样地这里我们只用到了一部分样本，而不是全部样本，这与线性回归不同。

在通过优化方法解得全部的拉格朗日乘子后，我们首先由的稳定性条件直接导出的解接着我们导出的解，注意到、，因此一定有，再由的互相松弛条件能得出，对于任意一个样本，有故而一旦，则必有；如果还有，进一步有为了尽可能多利用样本，利用更多的信息以减小噪声、误差等因素的影响，可以利用所有满足样本点计算值后取其算术平均值因此，我们可以写出分割超平面的解考虑映射到高维的变换与核函数，则注意代表训练集的第个数据，将一个新数据代入上式中的即可得到预测值，即

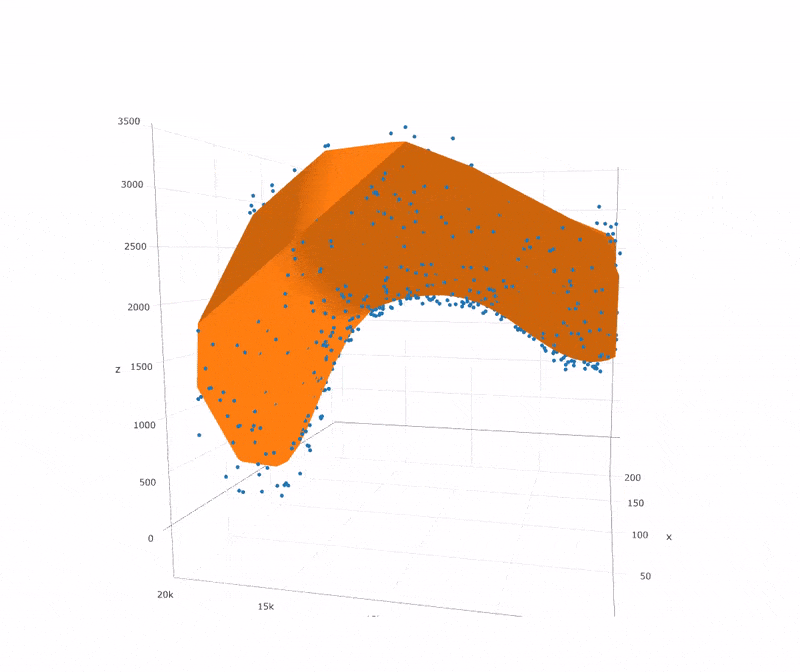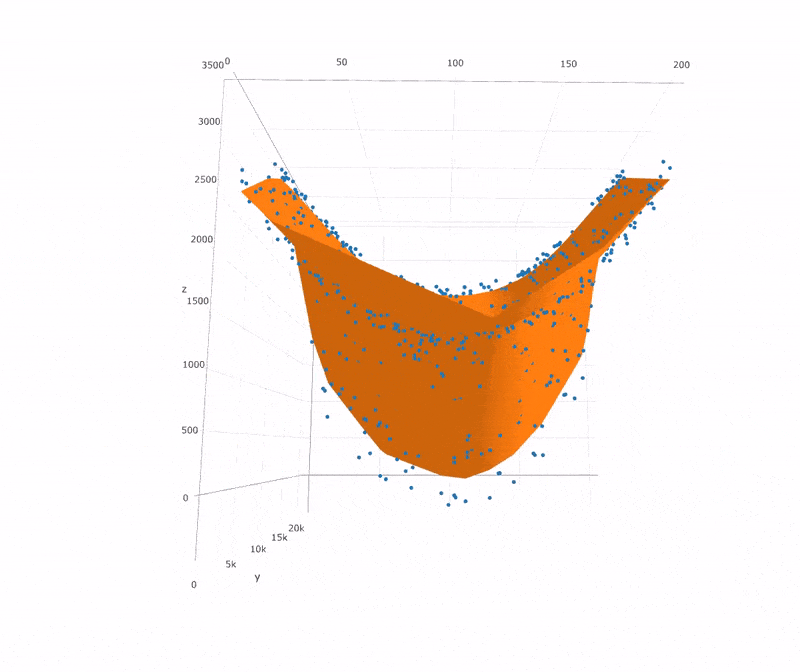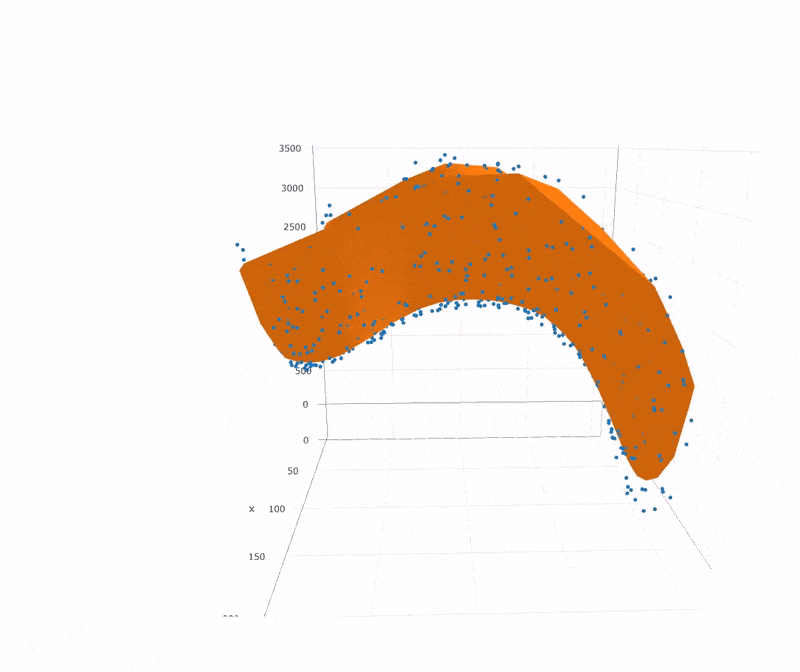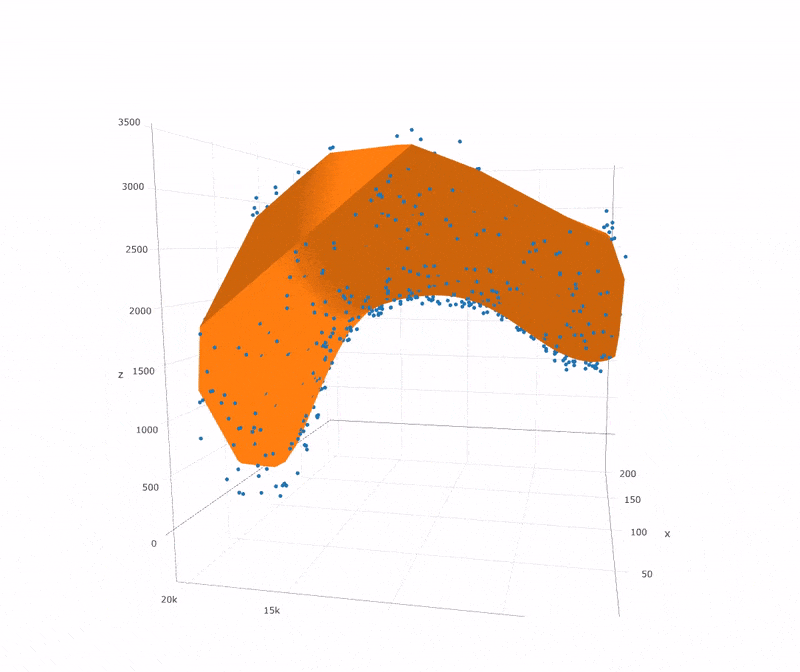
上图中Kernel Ridge Regression便是我们再熟悉不过的核化岭估计，在我的另一篇文档中，这是一篇关于回归分析（线性模型）的文档，如果以后有机会我会同样地把他转写成Markdown。这里的GPR为高斯过程回归，一种非参数模型。

可以看出，如果样本点有一段存在缺失，那么SVR的效果并不算太好。

3. 核方法广泛的运用场景

在SVM中我们通过核方法使得我们可以处理非线性可分的场景，那么我们可以把这个方法推广至其他应用场景，比如岭估计吗？

答案是可以的，首先我们需要一个被称为表示定理的定理。表示定理于2002年首次被证明，考虑利用Mercer定理构造，鉴于过程过于繁琐且复杂，证明略过。

表示定理：设是核函数对应的再生核Hilbert空间，是在上的范数。单调递增函数：和损失函数：，则问题的解一定可以表示成的形式。

表示定理虽然证明需要一定的理论基础，但他揭示了一个简单且强大的结论：只要正则化项单调递增，那么任何符合形式的优化问题的解一定可以写成核函数的线性组合的形式。由此可见，核方法并不是专属于SVM的特殊技巧，而是可以推而广之到LDA、OLS、岭估计等许多场景的一种方法。

4. LS-SVM与LS-SVR

4.1. 从SVR出发推导LS-SVM

LS-SVM（最小二乘支持向量机）于1999年由Sukyens提出，与之对应的是LS-SVR（最小二乘支持向量回归），其实这就是带核的岭回归。较之SVR，LS-SVR用范数代替了SVR的-不敏感损失函数，并用含松弛变量约束的不等式替换为用误差约束的等式，缺点是计算复杂度是样本复杂度的三次方量级，SVR相较之不会有严重的算力需求，但中等样本量大小下拟合效果不如LS-SVM。尽管原始优化问题从变形而来，仅用表示了RSS项的权重，但为了模型得到一个Bayes解释，在正则化项前也乘上系数并用比值表示结果，并把的等式约束带入目标式，得到对的广义拉格朗日函数求偏导令为，得到一个包含个拉格朗日乘子的线性方程组，所以LS-SVR并不是二次优化问题，而是一个线性方程组求解的问题其中是核矩阵， LS-SVR对噪声的敏感性强于SVR，模型的解比SVM更稠密（SVM的解相对较稀疏），随样本量增大线性方程组求解困难。

4.2. 从岭回归出发推导LS-SVM

在此之前，我们先简单介绍一下岭回归——一种最小二乘法的推广。对于普通岭回归，或者讲带有线性核的岭回归模型为记，模型的损失函数为从式利用拉格朗日乘子法，得到在Gauss–Марков定理成立的条件下，有 $有偏性：$

目前为止，我们简单介绍了岭回归。

欲在岭估计中应用核技巧，首先对的做高维映射变为矩阵：和前文推导类似地，最终可以得到不难看出，式中没有能让我们进行核函数处理的高维内积，这时我们需要Matrix Inversion Lemmas，他使得对令，，，并在等式两边同时右乘，得到如此一来我们构造出了；记核函数为：、样本的核矩阵为，其中为的方阵：但现在我们还没有办法进行预测，只有一个理论上估计的核方法（而且通常还不太可行，因为我们很难找到一个具体的合适映射）。假设通过训练集训练完模型以后，我们有新样本，记这批新样本的预测值为，由有由此一来我们便可以通过核技巧对样本进行非线性岭回归。

5. SMO算法的简单解释

SMO（Sequential Minimal Optimization），一般译作顺序最小化（优化）算法。

SMO算法每次选取一对拉格朗日乘子与，固定其他拉格朗日乘子，优化问题的约束针对这两个拉格朗日乘子可以简化为 $除去与对应的下标$ SMO将分解为一系列可能的最小子问题。步骤为：

选取一个拉格朗日乘子，应是中最大程度背离KKT条件的；
通过与，优化这对拉格朗日乘子；
转回步骤1.，直到收敛.

之所以令为最大程度背离KKT条件的一个拉格朗日乘子，是因为这样能使得的更新程度最大；当终止准则生效，应该在容许的误差范围内满足KKT条件，得到全部拉格朗日乘子数值解后、按前文提到到式子计算，最终得到超平面解析式。

经典文献参考：https://web.iitd.ac.in/~sumeet/tr-98-14.pdf

[John C. Platt, Sequential Minimal Optimization: A Fast Algorithm for Training Support Vector Machines, 1998]

6. R的e1071包与Python的sklearn库中的SVC&SVR

6.1. R（e1071 & tidymodel）

1	# omission

R - e1071官方文档：https://cran.r-project.org/web/packages/e1071/e1071.pdf

似乎'tidymodel'更方便？

6.2. Python（sklearn）

'''
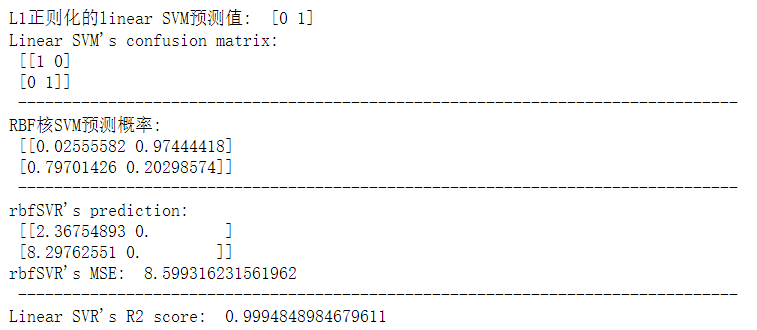
SVC（概率/非概率），参数：
C：C值，取值在0~1之间，用于软间隔的惩罚系数（软间隔影响权重），C值越大越严格，松弛变量越接近0，分类准确率高，可能造成过拟合（=1）
kernel：选择核函数（="rbf"），可选的有"rbf"、"linear"、"poly"即多项式核、用degree控制阶（=3），"sigmoid"
gamma：核函数系数，"rbf"、"poly"、"sigmoid"的参数（="auto"，即特征数倒数）
coef0：核函数的常系数，"poly"、"sigmoid"的参数
tol：终止准则的精度（=1e-3）
probability：是否输出概率（=False）
decision_function_shape：分类方式，可选"ovo"，"ovr"
class_weight：给每个类分别设置惩罚系数，不给就是1，等价于全设置为C（=None）
random_state
---------------------------------------------------
shrinking：是否只考虑支持向量（=True），理论上选择False不影响结果，但会使程序变慢
verbose：是否详细输出（=False）
---------------------------------------------------
方法：
.score(X, y)
.predict(X)
.predict_proba(X)
---------------------------------------------------
成员变量：
.decision_function  # 测试样本到超平面的距离
.n_support_
.support_  # 支持向量的索引
.support_vectors_
.coef_
.intercept_
***************************************************
特别地，LinearSVC还有一些可调整的参数，
penalty：超平面w”长度“的约束方式，"l1"、"l2"，选择"l1"得到的解稀疏，即非0分量尽可能少（="l2"）
loss：选择软间隔的损失函数，即”允许SVM犯错次数“计数器，"hinge"或"squared_hinge"，hinge loss(z)=max(0, 1-z)（="squared_hinge"）
dual：对偶问题，当样本数远大于特征数时，或许应该选择False？（=True）
multi_class："ovr"或"crammer_singe"（="ovr"）
max_iter：最大迭代次数（=1000）
'''
X = [[1, 2.5, 3], [4.5, 5, 5.5], [7, 8, 9.5], [10.5, 11, 12]]
y_class = [0, 0, 1, 1]
X_val = [[0, 1, 2.5], [13, 14.5, 16]]
y_class_val = [0, 1]


from sklearn.svm import SVC, LinearSVC
from sklearn.metrics import confusion_matrix

linearSVM = LinearSVC(penalty="l1", dual=False, max_iter=5000)
linearSVM.fit(X, y_class)

rbfSVM = SVC(C=0.8, kernel="rbf", probability=True)
rbfSVM.fit(X, y_class)

pre = linearSVM.predict(X_val)
CM_linearSVM = confusion_matrix(y_class_val, pre)
print("L1正则化的linear SVM预测值: ", pre)
print("Linear SVM's confusion matrix: \n", CM_linearSVM, "\n", "-"*80)


probability = rbfSVM.predict_proba(X_val)
print("RBF核SVM预测概率: \n", probability, "\n", "-"*80)

#######################################

# SVR与LinearSVR只接收一维输出，需要用MultiOutputRegressor转换
from sklearn.svm import SVR, LinearSVR
from sklearn.multioutput import MultiOutputRegressor
from sklearn.metrics import mean_squared_error, r2_score

y = [[2, 0.1], [5, 0], [8, 0.1], [11, -0.1]]
y_val = [[1, 0.1], [14, 0]]
y_singleValue = [2, 5, 8, 11]
y_val_singleValue = [1, 14]

rbfSVR = SVR(C=10, kernel="rbf")
rbfSVR_Multi = MultiOutputRegressor(rbfSVR)
rbfSVR_Multi.fit(X, y)

linearSVR = LinearSVR(C=3.31, max_iter=10000)
linearSVR.fit(X, y_singleValue)

prediction = rbfSVR_Multi.predict(X_val)
MSE_rbfSVR = mean_squared_error(y_val, prediction)
print("rbfSVR's prediction: \n", prediction)
print("rbfSVR's MSE: ", MSE_rbfSVR, "\n", "-"*80)

R2_linearSVR = r2_score(y_val_singleValue, linearSVR.predict(X_val))
print("Linear SVR's R2 score: ", R2_linearSVR)

运行结果：

参考：https://www.analyticsvidhya.com/bln/2017/09/understaing-support-vector-machine-example-code/

Python - sklearn官方文档：https://scikit-learn.org/stable/

6.3. MATLAB

MATLAB的“liblinear”与“libsvm”库的SVM/SVR算法都有相当不错的优化，二者皆由国立台湾大学林智仁教授设计开发，有数十种语言的发行版本，包括在R与Python上都有不错的性能，不仅仅在MATLAB适用；Liblinear较新，针对大数据设计，而Libsvm针对非线性分类SVM。

国立台湾大学 liblinear：https://www.csie.ntu.edu.tw/~cjlin/liblinear/

国立台湾大学 libsvm：https://www.csie.ntu.edu.tw/~cjlin/libsvm/